S曲线轨迹规划方法原理解析（附Python代码）

发布时间：2024-11-22 00:29

飞行轨迹规划与调整方法 #生活技巧# #数码产品使用技巧# #无人机飞行教学#

1. 引言

2.1 输入和输出

2.2 分段规划

2.3 实际求解

2.3.1 速度能够到最大（存在匀速阶段）

2.3.2 速度达不到最大（不存在匀速阶段）

3.代码实现

4. 参考文章

1. 引言

S曲线轨迹规划方法通过平滑的控制速度和加速度的变化，确保机器人在规划起点与目标点之间的平稳过渡，减少运动冲击，提高运动和控制精度。S曲线轨迹一般分为加加速（T1）、匀加速(T2)、减加速(T3)、匀速(T4)、加减速(T5)、匀减速(T6)、减减速(T7)七个阶段，又称为七段式S曲线，如图所示：

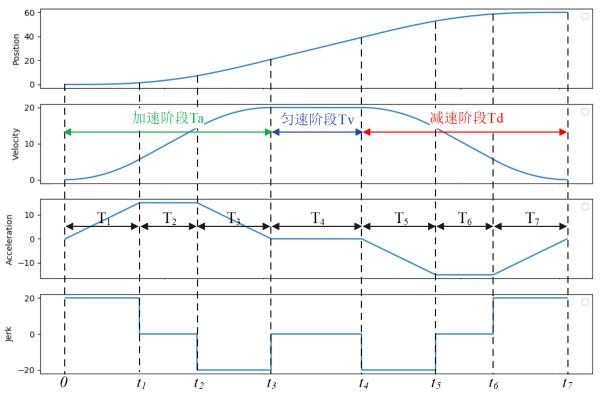
其中，图中 T1~T6 分别表示各运动阶段的持续时间，t1~t6 表示各运动阶段的过渡时刻，Ta表示加速运动持续时间，Tv表示匀速运动持续时间，Td表示减速运动持续时间。

2. 规划原理

2.1 输入和输出

七段式S曲线轨迹规划方法的输入和输出分别为：

输入：1.初始状态：初始位置 x0" role="presentation">x0、初始速度 v0" role="presentation">v0 ;

2.目标状态：目标位置 xg" role="presentation">xg、目标速度 vg" role="presentation">vg ;

3.运动限制：最大速度 vmax" role="presentation">vmax、最大加速度 amax" role="presentation">amax、最大加加速度(jerk) jmax" role="presentation">jmax ;

4.运动位移：s=xg−x0" role="presentation">s=xg−x0 ;

输出：位置轨迹 x(t)" role="presentation">x(t)、速度轨迹 v(t)" role="presentation">v(t)、加速度轨迹 a(t)" role="presentation">a(t) ，输出结果表示为一系列控制信号随时间 t 变化的函数。

2.2 分段规划

· 加加速度段T1(0<t≤t1" role="presentation">0<t≤t1): 加速度 a=0" role="presentation">a=0 以 j=jmax" role="presentation">j=jmax 线性增加至 a=amax" role="presentation">a=amax

a(t)=jmaxt" role="presentation">a(t)=jmaxt

v(t)=v0+12jmaxt2" role="presentation">v(t)=v0+12jmaxt2

x(t)=x0+16jmaxt3" role="presentation">x(t)=x0+16jmaxt3

· 匀加速度段T2(t1<t≤t2" role="presentation">t1<t≤t2): 加速度恒定，速度v=v(t1)" role="presentation">v=v(t1) 以 a=amax" role="presentation">a=amax 线性增加

a(t)=amax" role="presentation">a(t)=amax

v(t)=v(t1)+amax(t−t1)" role="presentation">v(t)=v(t1)+amax(t−t1)

x(t)=x(t1)+v(t1)(t−t1)+12amax(t−t1)2" role="presentation">x(t)=x(t1)+v(t1)(t−t1)+12amax(t−t1)2

· 减加速度段T3(t2<t⩽t3" role="presentation">t2<t⩽t3): 加速度 a=amax" role="presentation">a=amax 以 j=−jmax" role="presentation">j=−jmax 线性减小至0，速度增加至v=vmax" role="presentation">v=vmax

a(t)=amax−jmax(t−t2)" role="presentation">a(t)=amax−jmax(t−t2)

v(t)=vt2+amax(t−t2)−12jmax(t−t2)2" role="presentation">v(t)=vt2+amax(t−t2)−12jmax(t−t2)2

x(t)=x(t2)+v(t2)(t−t2)+12amax(t−t2)2−16jmax(t−t2)3" role="presentation">x(t)=x(t2)+v(t2)(t−t2)+12amax(t−t2)2−16jmax(t−t2)3

· 匀速段T4(t3<t⩽t4" role="presentation">t3<t⩽t4): 加速度 a=0" role="presentation">a=0， j=0" role="presentation">j=0， v=vmax" role="presentation">v=vmax

a(t)=0" role="presentation">a(t)=0

v(t)=v(t3)=vmax" role="presentation">v(t)=v(t3)=vmax

x(t)=x(t3)+vmax(t−t3)" role="presentation">x(t)=x(t3)+vmax(t−t3)

· 加减速段T5(t4<t⩽t5" role="presentation">t4<t⩽t5): 加速度以j=−jmax" role="presentation">j=−jmax 从0减少至a=−amax" role="presentation">a=−amax

a(t)=−jmax(t−t4)" role="presentation">a(t)=−jmax(t−t4)

v(t)=vmax−12jmax(t−t4)2" role="presentation">v(t)=vmax−12jmax(t−t4)2

x(t)=x(t4)+vmax(t−t4)−16jmax(t−t4)3" role="presentation">x(t)=x(t4)+vmax(t−t4)−16jmax(t−t4)3

· 匀减速段T6(t5<t⩽t6" role="presentation">t5<t⩽t6): 加速度 a=−amax" role="presentation">a=−amax， j=0" role="presentation">j=0

a(t)=−amax" role="presentation">a(t)=−amax

v(t)=v(t5)−amax(t−t5)" role="presentation">v(t)=v(t5)−amax(t−t5)

x(t)=x(t5)+v(t5)(t−t5)−12amax(t−t5)2" role="presentation">x(t)=x(t5)+v(t5)(t−t5)−12amax(t−t5)2

· 减减速段T7(t6<t⩽t7" role="presentation">t6<t⩽t7): 加速度以j=jmax" role="presentation">j=jmax 从 a=−amax" role="presentation">a=−amax 增加至 a=0" role="presentation">a=0

a(t)=−amax+jmax(t−t6)" role="presentation">a(t)=−amax+jmax(t−t6)

v(t)=v(t6)−12jmax(t−t6)2−amax(t−t6)" role="presentation">v(t)=v(t6)−12jmax(t−t6)2−amax(t−t6)

x(t)=x(t6)+v(t6)(t−t6)−12amax(t−t6)2−16jmax(t−t6)3" role="presentation">x(t)=x(t6)+v(t6)(t−t6)−12amax(t−t6)2−16jmax(t−t6)3

2.3 实际求解

在实际工程应用过程中，由于初速度、末速度、实际路径长度等限制，不能保证每次规划都存在上述完整的七段过程。所以又可以把 S 曲线的七段过程分为加速过程、匀速过程、减速过程三个阶段，这三个阶段的持续时间分别用Ta" role="presentation">Ta、Tv" role="presentation">Tv、Tj" role="presentation">Tj 表示。

2.3.1 速度能够到最大（存在匀速阶段）

(1)判断加速段能否达到最大加速度

首先判断加速阶段是否能够达到最大加速度amax" role="presentation">amax，其中，存在关系式：

v1=v0+12jmaxT12" role="presentation">v1=v0+12jmaxT12，amax=jmaxT1" role="presentation">amax=jmaxT1

由于加加速阶段(T1" role="presentation">T1)与减加速阶段(T3" role="presentation">T3)是对称的(即加速度 a" role="presentation">a 以 j=±jmax" role="presentation">j=±jmax 增加/减少到 a=amax" role="presentation">a=amax/a=0" role="presentation">a=0 的过程中时间相等，表示为Tj1" role="presentation">Tj1，速度增量相等)，在临界情况(刚好没有匀加速阶段T2" role="presentation">T2，加速度a" role="presentation">a达到amax" role="presentation">amax后马上减少)下，可以推导出：

v1−v0=amax22jmax" role="presentation">v1−v0=amax22jmax

vmax−v0=2(v1−v0)=amax2jmax" role="presentation">vmax−v0=2(v1−v0)=amax2jmax

vmax=v1+12jmaxTj12=v0+jmaxTj12" role="presentation">vmax=v1+12jmaxTj12=v0+jmaxTj12

则当(vmax−v0)jmax<amax2" role="presentation">(vmax−v0)jmax<amax2时，不能达到最大加速度amax" role="presentation">amax，也没有匀加速阶段，此时有关系式：

Tj1=vmax−v0jmax" role="presentation">Tj1=vmax−v0jmax

Ta=2Tj1" role="presentation">Ta=2Tj1

此时，系统最大加速度为alim=jmaxTj1" role="presentation">alim=jmaxTj1 。

当(vmax−v0)jmax>amax2" role="presentation">(vmax−v0)jmax>amax2时，能达到最大加速度amax" role="presentation">amax，存在匀加速阶段(T2" role="presentation">T2)，此时有关系式：

Tj1=amaxjmax" role="presentation">Tj1=amaxjmax

vmax−v0=12jmaxTj12+amaxT2+12jmaxTj12=jmaxTj12+amaxT2" role="presentation">vmax−v0=12jmaxTj12+amaxT2+12jmaxTj12=jmaxTj12+amaxT2

Ta=2Tj1+T2" role="presentation">Ta=2Tj1+T2

进一步得到：

T2=vmax−v0a−Tj1" role="presentation">T2=vmax−v0a−Tj1

Ta=Tj1+vmax−v0amax" role="presentation">Ta=Tj1+vmax−v0amax

(2)判断减速段能否达到最大减速度

同理，减减速阶段(T7" role="presentation">T7)与加减速阶段(T5" role="presentation">T5)是对称的(即加速度 a" role="presentation">a 以 j=±jmax" role="presentation">j=±jmax 增加/减少到 a=amax" role="presentation">a=amax/a=0" role="presentation">a=0 的过程中时间相等，表示为Tj2" role="presentation">Tj2，速度增量相等)，临界情况为刚好没有匀减速阶段T6" role="presentation">T6。
同理，当 (vmax−vg)jmax<amax2" role="presentation">(vmax−vg)jmax<amax2 时，达不到最大减速度 a=−amax" role="presentation">a=−amax，存在：

Tj2=vmax−vgjmax" role="presentation">Tj2=vmax−vgjmax

Td=2Tj2" role="presentation">Td=2Tj2

当 (vmax−vg)jmax>amax2" role="presentation">(vmax−vg)jmax>amax2 时，可以达到最大减速度 a=−amax" role="presentation">a=−amax，存在：

Tj2=amaxjmax" role="presentation">Tj2=amaxjmax

Td=Tj2+vmax−vgamax" role="presentation">Td=Tj2+vmax−vgamax

(3) 计算匀速阶段时间

由于加速阶段中加速过程的对称性，加速阶段平均速度可以表示为v0+vmax2" role="presentation">v0+vmax2，同理减速阶段平均速度为vmax+vg2" role="presentation">vmax+vg2，则可以求出匀速阶段持续时间Tv" role="presentation">Tv：

v0+vmax2Ta+vmaxTv+vmax+vg2Td=s" role="presentation">v0+vmax2Ta+vmaxTv+vmax+vg2Td=s

Tv=svmax−Ta2(1+v0vmax)−Td2(1+vgvmax)" role="presentation">Tv=svmax−Ta2(1+v0vmax)−Td2(1+vgvmax)

如果Tv>0" role="presentation">Tv>0，则存在匀速阶段，可以按照上述各阶段公式，求出七个阶段各段的位置、速度、加速度函数。如果Tv<0" role="presentation">Tv<0，则不存在匀速阶段，系统达不到最大速度vmax" role="presentation">vmax。

2.3.2 速度达不到最大（不存在匀速阶段）

Tv<0" role="presentation">Tv<0，不存在匀速阶段，系统达不到最大速度vmax" role="presentation">vmax。存在：

Tj1=Tj2=amaxjmax" role="presentation">Tj1=Tj2=amaxjmax

Ta=amax2jmax−2v0+Δ2amax" role="presentation">Ta=amax2jmax−2v0+Δ2amax

Td=amax2jmax−2vg+Δ2amax" role="presentation">Td=amax2jmax−2vg+Δ2amax

Δ=amax4j2+2(v02+vg2)+amax(4s−2(v0+vg)amaxjmax)" role="presentation">Δ=amax4j2+2(v02+vg2)+amax(4s−2(v0+vg)amaxjmax)

其中，Δ" role="presentation">Δ推导参考【4】，此时，关于系统能否达到最大加速度a=±amax" role="presentation">a=±amax，需要讨论Ta" role="presentation">Ta与2Tj1" role="presentation">2Tj1，Td" role="presentation">Td与2Tj2" role="presentation">2Tj2大小关系。

当 Ta≥2Tj1" role="presentation">Ta≥2Tj1 且 Td≥2Tj2" role="presentation">Td≥2Tj2 时，系统不能达到最大速度vmax" role="presentation">vmax，但可以达到最大加速度，存在：

vmax′=v0+amax(Ta−Tj1)" role="presentation">vmax′=v0+amax(Ta−Tj1)

当 Ta<2Tj1" role="presentation">Ta<2Tj1 且 Td<2Tj2" role="presentation">Td<2Tj2 时，系统不能达到最大速度vmax" role="presentation">vmax，也达不到最大加速度，此时需逐渐减少设定的最大加速度amax" role="presentation">amax，直至满足 Ta≥2Tj1" role="presentation">Ta≥2Tj1 且 Td≥2Tj2" role="presentation">Td≥2Tj2 为止。

3.代码实现

import numpy as np

import matplotlib.pyplot as plt

x_0 = 0

x_g = 60

v_max = 20

v_0 = 0

v_g = 0

a_max = 15

j_max = 20

count = 0

if (v_max - v_0) * j_max < a_max ** 2:

if v_0 > v_max:

Tj1 = 0

Ta = 0

alima = 0

else:

Tj1 = np.sqrt((v_max - v_0) / j_max)

Ta = 2 * Tj1

alima = Tj1 * j_max

else:

Tj1 = a_max / j_max

Ta = Tj1 + (v_max - v_0) / a_max

alima = a_max

if (v_max - v_g) * j_max < a_max ** 2:

Tj2 = np.sqrt((v_max - v_g) / j_max)

Td = 2 * Tj1

alimd = Tj2 * j_max

else:

Tj2 = a_max / j_max

Td = Tj2 + (v_max - v_g) / a_max

alimd = a_max

Tv = (x_g - x_0) / v_max - Ta / 2 * (1 + v_0 / v_max) - Td / 2 * (1 + v_g / v_max)

T = Tv + Ta + Td

p = []

vc = []

ac = []

jc = []

if Tv > 0:

vlim = v_max

T = Tv + Ta + Td

else:

Tv = 0

amax_org = a_max

delta = (a_max ** 4) / (j_max ** 2) + 2 * (v_0 ** 2 + v_g ** 2) + a_max * (4 * (x_g - x_0) - 2 * a_max / j_max * (v_0 + v_g))

Tj1 = a_max / j_max

Ta = (a_max ** 2 / j_max - 2 * v_0 + np.sqrt(delta)) / (2 * a_max)

Tj2 = a_max / j_max

Td = (a_max ** 2 / j_max - 2 * v_g + np.sqrt(delta)) / (2 * a_max)

vlim = v_0 + (Ta - Tj1) * alima

while Ta < 2 * Tj1 or Td < 2 * Tj2:

count += 1

a_max -= amax_org * 0.1

alima = a_max

alimd = a_max

if a_max > 0:

delta = (a_max ** 4) / (j_max ** 2) + 2 * (v_0 ** 2 + v_g ** 2) + a_max * (4 * (x_g - x_0) - 2 * a_max / j_max * (v_0 + v_g))

else:

delta = (a_max ** 4) / (j_max ** 2) + 2 * (v_0 ** 2 + v_g ** 2) - a_max * (4 * (x_g - x_0) - 2 * a_max / j_max * (v_0 + v_g))

Tj1 = a_max / j_max

Ta = (a_max ** 2 / j_max - 2 * v_0 + np.sqrt(delta)) / (2 * a_max)

Tj2 = a_max / j_max

Td = (a_max ** 2 / j_max - 2 * v_g + np.sqrt(delta)) / (2 * a_max)

vlim = v_0 + (Ta - Tj1) * alima

vlima = vlim

vlimb = v_g - (Td - Tj2) * alimd

print("调整后信息:")

print("TJ1:",Tj1)

print("Ta:",Ta)

print("Td",Td)

print("a_max:",a_max)

if Ta < 0 or Td < 0:

if v_0 > v_g:

Ta = 0

Tj1 = 0

alima = 0

Td = 2 * (x_g - x_0) / (v_g + v_0)

Tj2 = (j_max * (x_g - x_0) - np.sqrt(j_max * (j_max * (x_g - x_0) ** 2 + (v_g + v_0) ** 2 * (v_g - v_0)))) / (j_max * (v_g + v_0))

alimd = -j_max * Tj2

vlim = v_g - (Td - Tj2) * alimd

alimd = -alimd

else:

Td = 0

Tj2 = 0

Ta = 2 * (x_g - x_0) / (v_g + v_0)

Tj1 = (j_max * (x_g - x_0) - np.sqrt(j_max * (j_max * (x_g - x_0) ** 2 - (v_g + v_0) ** 2 * (v_g - v_0)))) / (j_max * (v_g + v_0))

alima = j_max * Tj1

vlim = v_0 + (Ta - Tj1) * alima

print(Tj1)

print(Tj2)

print(Ta)

print(Td)

print("565")

print(alima)

print(alimd)

T = Tv + Ta + Td

for t in np.arange(0, T, 0.001):

if 0 <= t < Tj1:

x = x_0 + v_0 * t + j_max * t ** 3 / 6

p.append(x)

v = v_0 + j_max * t ** 2 / 2

vc.append(v)

a = j_max * t

ac.append(a)

jc.append(j_max)

elif Tj1 <= t < (Ta - Tj1):

x = x_0 + v_0 * t + alima / 6 * (3 * t ** 2 - 3 * Tj1 * t + Tj1 ** 2)

p.append(x)

v = v_0 + alima * (t - Tj1 / 2)

vc.append(v)

a = alima

ac.append(a)

jc.append(0)

elif (Ta - Tj1) <= t < Ta:

x = x_0 + (vlim + v_0) * Ta / 2 - vlim * (Ta - t) + j_max * (Ta - t) ** 3 / 6

p.append(x)

v = vlim - j_max * (Ta - t) ** 2 / 2

vc.append(v)

a = j_max * (Ta - t)

ac.append(a)

jc.append(-j_max)

elif Ta <= t < (Ta + Tv):

x = x_0 + (vlim + v_0) * Ta / 2 + vlim * (t - Ta)

p.append(x)

v = vlim

vc.append(v)

a = 0

ac.append(0)

jc.append(0)

elif (T - Td) <= t < (T - Td + Tj2):

x = x_g - (vlim + v_g) * Td / 2 + vlim * (t - T + Td) - j_max * (t - T + Td) ** 3 / 6

p.append(x)

v = vlim - j_max * (t - T + Td) ** 2 / 2

vc.append(v)

a = -j_max * (t - T + Td)

ac.append(a)

jc.append(-j_max)

elif (T - Td + Tj2) <= t < (T - Tj2):

x = x_g - (vlim + v_g) * Td / 2 + vlim * (t - T + Td) - alimd / 6 * (3 * (t - T + Td) ** 2 - 3 * Tj2 * (t - T + Td) + Tj2 ** 2)

p.append(x)

v = vlim - alimd * (t - T + Td - Tj2 / 2)

vc.append(v)

a = -alimd

ac.append(a)

jc.append(0)

elif (T - Tj2) <= t < T:

x = x_g - v_g * (T - t) - j_max * (T - t) ** 3 / 6

p.append(x)

v = v_g + j_max * (T - t) ** 2 / 2

vc.append(v)

a = -j_max * (T - t)

ac.append(a)

jc.append(j_max)

t = np.arange(0, T, 0.001)

plt.figure(figsize=(12, 8))

plt.subplot(4, 1, 1)

plt.plot(t, p)

plt.ylabel('Position')

plt.legend()

plt.subplot(4, 1, 2)

plt.plot(t, vc)

plt.ylabel('Velocity')

plt.legend()

plt.subplot(4, 1, 3)

plt.plot(t, ac)

plt.ylabel('Acceleration')

plt.xlabel('Time')

plt.legend()

plt.subplot(4, 1, 4)

plt.plot(t, jc)

plt.ylabel('Jerk')

plt.xlabel('Time')

plt.legend()

plt.show()

运行结果：

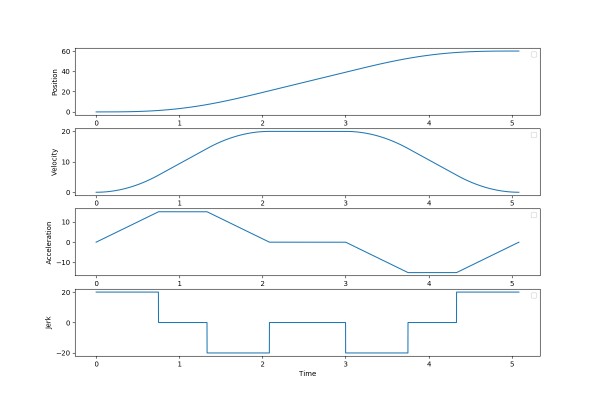
4. 参考文章

[1]一文教你快速搞懂速度曲线规划之S形曲线（超详细+图文+推导+附件代码）_s型速度曲线-CSDN博客

[2]【机器人学】5-2.六自由度机器人轨迹规划-速度规划- S型曲线【附MATLAB代码】_scurve速度规划 matlab代码-CSDN博客

[3]分段式S形速度规划算法_s型加减速曲线不存在匀加速-CSDN博客

[4]田军锋,林浒,姚壮,等.数控系统S型曲线加减速快速规划研究[J].小型微型计算机系统,2013,34(01):168-172.

网址：S曲线轨迹规划方法原理解析（附Python代码） https://www.yuejiaxmz.com/news/view/182606

⬅️上一篇：重要紧急

➡️下一篇：掌控：如何规划自己的时间和生活

S曲线轨迹规划方法原理解析（附Python代码）

1. 引言

2.1 输入和输出

2.2 分段规划

2.3 实际求解

3.代码实现

4. 参考文章

相关内容

随便看看

最新动态分享

热点动态分享

专题

推荐动态分享