基于ADMM的智能电网电力调度优化分布式在线算法

发布时间：2024-11-26 00:40

物联网在公共服务中，如智能电网、智能电网，可以实现电力资源的优化分配和用户用电行为的分析。 #生活知识# #科技生活# #科技改变生活# #物联网#

基于ADMM的智能电网电力调度优化分布式在线算法
ADMM-Based Distributed OnlineAlgorithm for Power Dispatching Optimization of Smart Grid

1. 引言

智能电网是将信息技术、通信技术、计算机技术、先进的电力电子技术、可再生能源发电技术和原有的输配电基础设施高度集成的新型电网，被世界各国视为推动经济发展和产业革命，实现可持续发展的新基础和新动力 [1]。

近年来，随着智能电网的发展，智能电网至今仍存在很多问题有待解决。全面实现电网的智能化建设是一个循序渐进的过程，而在这过程中，需要我们去不断地发现问题并解决问题，使得智能电网的建设慢慢地满足要求和逐步地完善。这样主要是为了对智能电网中各个组成元素实现他们的最大效益，解决各个层面的矛盾。目前阅读相关文献了解到，目前智能电网的相关研究仍在为了实现各层间的利益最大化以及解决各个层间隐私泄露问题而极力探索和创新。对于该类问题已经有很多创新性的研究：研究终端用户与电网的双向能量交易问题，目的是最大化用户的收益，采用李雅普诺夫优化理论提出的实时算法复杂度低，且不需要知道用户能量需求、电价变化和可再生源到达的统计特性 [2]、数据聚合技术在加密用户数据后再进行聚合，比传统的聚合方法成本更低、效率更高；群签名可以验证用户身份，保护用户隐私，并且最小化通信开销 [3]、基于遗传算法提出一种多种类型可控电器的G-DSM算法，将负载调度问题定义为成本最小化问题，并用遗传算法求解，结合从用户侧获取的电力大数据对用户的电力需求进行规划，降低了用户的花销以及峰值电力负载，从而避免电力资源的浪费，提高了电网的工作效率 [4]、采用在线对偶方法求解社会福利最大化模型的拉格朗日乘子，以此来确定电网电价 [5]。针对相关问题，本文提出了基于ADMM的分布式算法，该模型以历史信息为约束条件，为下一时刻电量实现分配最优。模型主要通过对各个元素的敏感信息进行分离并求解各个子问题，既实现有效维护各方隐私信息，也达到电网中各个关键元素利益最大化的目的。

2. 系统模型

2.1. 系统定义

在智能电网的环境中，电网分配系统主要由三个关键部分构成：电网运营商、供电商及用户。这三者之间通过相关智能设备进行信息的交互，交互的方式是：所有的智能设备通过一些无线网等相关信息交互方式与电网运营商相连接。在每次的能源分配的时间周期内，智能设备和电网运营商之间交互智能电网的状态和相关控制信息，以此来最大化用户的效用函数、最小化运营成本及平滑电网总负载方差。然后，供电商相应地将电力进行传输并分发给用户。

在本文中，我们对下面一些变量进行相关的定义：

在智能电网中，电力分配的时间周期T可分为多个时刻 t∈T→={1,2,⋯,T}" role="presentation">t∈T→={1,2,⋯,T}，其中 T→" role="presentation">T→ 为所有时间点的集合。用户i在每个t时刻的用电量为 pi(t)" role="presentation">pi(t)，同时 N¯={1,2,⋯,N}" role="presentation">N¯={1,2,⋯,N} 为用户集。设定对于每个用户i在每个时刻t的电量消耗为：

p=[pi,min(t),pi,max(t)]" role="presentation">p=[pi,min(t),pi,max(t)] (1)

其中 pi,min(t)" role="presentation">pi,min(t) 为每个用户i在时刻t的实际最小需求电量， pi,max(t)" role="presentation">pi,max(t) 为每个用户i在时刻t的实际最大需求电量。我们认为 pi(t)∈p" role="presentation">pi(t)∈p，且p非负凸集。

2.2. 用户效用函数

在本文中，我们认为在智能电网中用户的行为是相互独立的。在不同的时间内用户有着不同的偏好和用电规律。这主要体现在如天气、不同功率用电器的使用及用电规模等情况。对此，我们采用效用函数 U(pi(t),wi(t))" role="presentation">U(pi(t),wi(t)) 代表用户的行为偏好 [5]。其中 wi(t)" role="presentation">wi(t) 为用户i的偏好参数，该参数代表不同用户在如上述的不同情况下的不同时间内的偏好，且在[0,1]区间内随机取值。而对于本文采用的用户效用函数可以用二次函数表示，即：

U(pi(t),wi(t))={wi(t)pi(t)−18pi(t)2      0≤pi(t)≤4wi(t)4wi(t)                           pi(t)>4wi(t)" role="presentation">U(pi(t),wi(t))={wi(t)pi(t)−18pi(t)2 0≤pi(t)≤4wi(t)4wi(t) pi(t)>4wi(t) (2)

2.3. 供应成本函数

对于供电商来说，考虑在满足需求的条件下供应成本问题是首当其冲的。我们通过阅读文献了解到：在智能电网中，供电商的成本问题主要与电网负载成正相关。当电网负载越大，供应成本就越高，反之亦然。这主要表现在：当在一些情况下，用电量逐渐临近点电网负载时，电网运营商不得要求供电商更多电量的供应以避免用户的用电问题，这必然增加了供电商的供电成本。因此，在本文中应用一个递增且严格凸的二次函数近似表示为供电成本函数 [6] [7] [8]，具体如下：

C(g(t))=a⋅g(t)2+b⋅g(t)+c" role="presentation">C(g(t))=a⋅g(t)2+b⋅g(t)+c (3)

其中， a,b,c" role="presentation">a,b,c 是预先为电网选择的，且 a,b,c≥0" role="presentation">a,b,c≥0。 g(t)" role="presentation">g(t) 定义为供电商在时刻t的电力总生产量，即供电商在低供电成本的情况下需要满足用户的足够用电量。

另外，我们认为供电商在某一时刻t满足用户需求电量时的最大电力生产量为 gmax(t)" role="presentation">gmax(t)，于是：

g(t)min≤g(t)≤gmax(t)" role="presentation">g(t)min≤g(t)≤gmax(t) (4)

在这里我们认为， g(t)∈G=[gi,min(t),gi,max(t)]" role="presentation">g(t)∈G=[gi,min(t),gi,max(t)]，而 gi,min(t)≥∑i∈N¯pi(t)" role="presentation">gi,min(t)≥∑i∈N¯pi(t)。另外，由于成本函数 C(·)" role="presentation">C(·) 为严格凸且递增的，所以供电商需要通过调整发电量 g(t)" role="presentation">g(t) 来控制其成本。

3. 问题构建和方法介绍

在本节中，我们需要对文献提出的离线算法做一个基本介绍，以此来引出后文中基于ADMM算法的分布式在线算法及其较离线算法和其他研究提出的分布式在线算法，并进行相关比较。

离线算法

在智能电网环境中，我们考虑到问题模型中涉及三个关键的因素：用户、电网运营商和供电商。在这种考虑下，我们的目的是：1) 最大化用户的效用函数；2) 最小化供电成本；3) 平滑电网总负载。

在离线场景中，电网运营商需要对用户的偏好参数 wi(t)" role="presentation">wi(t) 和供电商的总发电量 g(t)" role="presentation">g(t) 有着预先的信息掌控。在这里，设 Pi(t)" role="presentation">Pi(t) 为用户i在t时刻的用电量， Pi∗(t)" role="presentation">Pi∗(t) 为用户在t时刻的最优用电量，且 Pi∗(t),Pi(t)∈p" role="presentation">Pi∗(t),Pi(t)∈p。于是，对所有时刻 t∈T→" role="presentation">t∈T→，离线问题为：

min:∑t∈T→[C(g(t))−∑i∈N¯U(Pi(t),wi(t))]+αT2var(∑i∈N¯P→i)s.t. ∑i∈N¯[Pi(t)+αα+t[Pi∗(t−1)−Pi∗(t−2)]+]=g(t)" role="presentation">min:∑t∈T→[C(g(t))−∑i∈N¯U(Pi(t),wi(t))]+αT2var(∑i∈N¯P→i)s.t. ∑i∈N¯[Pi(t)+αα+t[Pi∗(t−1)−Pi∗(t−2)]+]=g(t) (5)

令 Rt=αα+t[∑i∈N¯(Pi∗(t−1)−P^i∗(t−2))]+" role="presentation">Rt=αα+t[∑i∈N¯(Pi∗(t−1)−P^i∗(t−2))]+，代表把前两次时间的最优用电量作为下一时间的影响因素，而 [•]+" role="presentation">[•]+ 表示：为正时取相应的值，否则为零。这是用户的历史用电情况。其中 var(⋅)" role="presentation">var(⋅) 为方差函数，即：

var(∑i∈N¯P→i)=1T∑t∈T→(∑i∈N¯Pi(t)−1T∑k∈T→∑i∈N¯Pi(k))2" role="presentation">var(∑i∈N¯P→i)=1T∑t∈T→(∑i∈N¯Pi(t)−1T∑k∈T→∑i∈N¯Pi(k))2 (6)

在式(5)中由有三个关键主要部分组成，分别是供电成本，用户的效用函数和电网负载方差。在目标函数的第三部分中，存在一个权衡参数 α" role="presentation">α，其作用是在智能电网中对用户权益和电网负载进行权衡。而在约束条件中我们认为前时刻的用电量作为一个影响因子作用于下一时刻的用电量，由此，我们构建了如式(5)中的约束。

在离线算法中，我们在前文中提到各个用户的用电量 Pi(t)" role="presentation">Pi(t) 是相互独立的。那么式(6)可以重新写为： var(∑i∈N¯P→i)=∑i∈N¯var(P→i)" role="presentation">var(∑i∈N¯P→i)=∑i∈N¯var(P→i)。接下来，说明离线算法是一个凸优化问题，这是因为目标函数中的效用函数 U(⋅)" role="presentation">U(⋅) 是一个凹函数，供电成本函数 C(⋅)" role="presentation">C(⋅) 和方差函数 var(⋅)" role="presentation">var(⋅) 均为凸函数。同样，由于方差函数 var(⋅)" role="presentation">var(⋅) 的凸性，文献 [9] 已给出证明离线函数有唯一解。而在离线算法中，文献 [9] 介绍了该算法在满足KKT条件下能够得到每时刻t每个用户i的最优解，其中用电均值为 P¯i∗=1T∑k=1TPi∗(k)" role="presentation">P¯i∗=1T∑k=1TPi∗(k)。而在该算法中，所有信息都是需先

验知的，但是现实智能电网环境中，预先获取所有信息是不太可能的。

于是，对于这类问题，文献 [9] 和 [10] 分别提出了在线算法(Online Algorithm)和分布式在线算法(Distributed Online Algorithm, DOA)。这两种算法分别通过在线方式和分布式解决了离线算法存在的预知信息问题，而且DOA算法通过拉格朗日将原始问题转化为对偶问题，进一步地解决了在线算法上用户隐私信息泄露的不足，但是DOA方法中仍存在一些性能上的不足。由此，在下面章节，我们提出了一种基于ADMM的分布式在线算法(Distributed Online Algorithm Based on ADMM，简称DOAA)，该算法既继承了在线算法预先不需要所有信息的优点，同时也达到了DOA算法的分布式求解的效果，并在性能比DOA算法更具优势。

4. 基于ADMM的分布式在线算法

算法介绍

ADMM 算法是一种用于求解具有可分解结构的凸优化问题的重要方法，由于其处理速度快、收敛性能好，所以该算法在很多研究领域都得到广泛的应用和认可 [11]。ADMM算法一般用于等式约束的凸优化问题，具体如下：

min f(x)+g(z)s.t.  Ax+Bz=c" role="presentation">min f(x)+g(z)s.t. Ax+Bz=c (7)

其中 f(x)" role="presentation">f(x) 和 g(z)" role="presentation">g(z) 均为凸函数，x、z为两组变量。

由此构建增广拉格朗日函数：

L(x,z,λ)=f(x)+g(z)+λT(Ax+Bz−c)+ρ2‖Ax+Bz−c‖22" role="presentation">L(x,z,λ)=f(x)+g(z)+λT(Ax+Bz−c)+ρ2‖Ax+Bz−c‖22 (8)

式(8)中： λ" role="presentation">λ 为增广拉格朗日对偶变量， ρ" role="presentation">ρ 为惩罚系数。由此可以把约束问题转化为无约束问题。

根据式(8)可得到ADMM的迭代求解方程：

{xk+1=argminxLρ(x,zk,λk)zk+1=argminzLρ(xk+1,z,λk)λk+1=λk+ρ(Axk+1+Bzk+1−c)" role="presentation">{xk+1=argminxLρ(x,zk,λk)zk+1=argminzLρ(xk+1,z,λk)λk+1=λk+ρ(Axk+1+Bzk+1−c) (9)

不难发现，在更新x的第k + 1次迭代需要z的第k次迭代结果，而在更新z的第k + 1次迭代需要x的第k + 1次迭代结果，最后更新 λ" role="presentation">λ 的第k + 1次迭代需要 λ" role="presentation">λ 的第k次迭代结果及x的第k + 1次迭代结果和z的第k次迭代结果。

由此，我们把离线问题进行更改，对于整个 t∈T→={1,2,⋯,T}" role="presentation">t∈T→={1,2,⋯,T} ：

min:∑t∈T→C(g(t))+αT2var(∑i∈N¯P→i(t))−∑t∈T→∑i∈N¯U(Pi(t),wi(t))s.t.  ∑i∈N¯Pi(t)+Rt=g(t)" role="presentation">min:∑t∈T→C(g(t))+αT2var(∑i∈N¯P→i(t))−∑t∈T→∑i∈N¯U(Pi(t),wi(t))s.t. ∑i∈N¯Pi(t)+Rt=g(t) (10)

根据ADMM算法在的优化规则，可以将总用电量 g(t)" role="presentation">g(t) 、用电量 Pi(t)" role="presentation">Pi(t) 两个目标函数的变量之间相互迭代，进行求解。然后，我们结合文献 [9] 提出的离线问题转化为在线问题的引理和方法，即：

引理1：对于 T→∞" role="presentation">T→∞，每个用户i的实际用电量和最优电力分配的关系：

limT→∞1T∑t=1T(pi∗(t)−p^i(T))=0" role="presentation">limT→∞1T∑t=1T(pi∗(t)−p^i(T))=0 (11)

我们知道在时间趋于无穷大时，最优电力分配量 pi∗(t)" role="presentation">pi∗(t) 是逐渐收敛于 p^i(T)" role="presentation">p^i(T)。

然后，对 p^i(t)" role="presentation">p^i(t) 更新：

p^i(t)=p^i(t−1)+αα+t(pi∗(t)−p^i(t−1))" role="presentation">p^i(t)=p^i(t−1)+αα+t(pi∗(t)−p^i(t−1)) (12)

从文献 [9] 得知，当 t→∞" role="presentation">t→∞ 时， p^i(t)" role="presentation">p^i(t) 是渐近收敛于定点 P¯i∗" role="presentation">P¯i∗。

由此我们可以将离线问题转化为在线问题，具体如下：

对时间序列 t∈T→={1,2,⋯,T}" role="presentation">t∈T→={1,2,⋯,T} 有：

minC(g(t))+α2∑i∈N¯(pi(t)−p^i(t−1))2−∑i∈N¯U(pi(t),wi(t))s.t.  ∑i∈N¯[pi(t)+αα+t[pi∗(t−1)−pi∗(t−2)]+]=g(t)" role="presentation">minC(g(t))+α2∑i∈N¯(pi(t)−p^i(t−1))2−∑i∈N¯U(pi(t),wi(t))s.t. ∑i∈N¯[pi(t)+αα+t[pi∗(t−1)−pi∗(t−2)]+]=g(t) (13)

于是增广拉格朗日为：

Lρ(pi(t),g(t),λ(t))=∑t∈T→C(g(t))+∑i∈N¯(α2(pi(t)−p^i(t−1))−U(pi(t),wi(t))) +λ(t)(∑i∈N¯[pi(t)+αα+t[pi∗(t−1)−p^i(t−2)]+]−g(t)) +ρ2‖∑i∈N¯[pi(t)+αα+t[pi∗(t−1)−pi∗(t−2)]+]−g(t)‖22" role="presentation">Lρ(pi(t),g(t),λ(t))=∑t∈T→C(g(t))+∑i∈N¯(α2(pi(t)−p^i(t−1))−U(pi(t),wi(t))) +λ(t)(∑i∈N¯[pi(t)+αα+t[pi∗(t−1)−p^i(t−2)]+]−g(t)) +ρ2‖∑i∈N¯[pi(t)+αα+t[pi∗(t−1)−pi∗(t−2)]+]−g(t)‖22 (14)

该模型中的 ∑i∈N¯(pi(t)−p^i(t−1))2" role="presentation">∑i∈N¯(pi(t)−p^i(t−1))2 与离线算法中的方差 var(P→i)" role="presentation">var(P→i) 近似，这是由于 p^i(t)" role="presentation">p^i(t) 渐近收敛于定点 P¯i∗" role="presentation">P¯i∗。而在此模型中，我们发现尽管该模型与文献 [9] 中的模型仅在约束条件中加了有关历史信息的变量 rt=αα+t∑i∈N¯[pi∗(t−1)−pi∗(t−2)]+" role="presentation">rt=αα+t∑i∈N¯[pi∗(t−1)−pi∗(t−2)]+， rt" role="presentation">rt 表示在线情况下随着时间变化的历史信息，同时也为用户用电需求做一个保障，而这并未改变模型原本的性质，所以该模型仍然满足文献 [9] 的各个条件。同时，在线最优解也是渐近收敛到离线最优解的，所以该模型与已有的模型等价。我们从文献 [9] 了解到在线算法中存在的缺点：在该模型中前一项包含着电网运营商所需的信息—总用电量 g(t)" role="presentation">g(t)，而后两项包涉及到用户的用电量 pi(t)" role="presentation">pi(t) 和偏好系数 wi(t)" role="presentation">wi(t) 的隐私信息，再者我们不能很好地对这些耦合信息进行有效分离来分别求解，这主要由于在约束条件中仍包含着两者的信息。

对此，本文借鉴文献 [10] 的对偶分离的思想，并根据ADMM的求解方法和考虑其优化性能，然后结合式(14)可以得到如下方程：

对于每个时刻t，有：

{pik+1=argminpi∈pLρ(pi,gk,λk)gk+1=argming∈GLρ(pik+1,g,λk)λtk+1=λtk+ρ‖∑i∈N¯pik+1+rt−gk+1‖22" role="presentation">{pik+1=argminpi∈pLρ(pi,gk,λk)gk+1=argming∈GLρ(pik+1,g,λk)λtk+1=λtk+ρ‖∑i∈N¯pik+1+rt−gk+1‖22 (15)

然后，根据ADMM算法的原理，当原始残差 γk+1" role="presentation">γk+1 和对偶残差 sk+1" role="presentation">sk+1 同时小于收敛阈值 ε" role="presentation">ε 时，上述迭代过程终止。即：

{‖γk+1‖2=‖∑ipik+1+rt−gk+1‖2≤εprim‖sk+1‖2=ρ‖gk+1−gk‖2≤εdual" role="presentation">{‖γk+1‖2=‖∑ipik+1+rt−gk+1‖2≤εprim‖sk+1‖2=ρ‖gk+1−gk‖2≤εdual (16)

式中 εprim" role="presentation">εprim 、 εdual" role="presentation">εdual 分别是原始残差的收敛阈值和对偶残差的收敛阈值，在后文中均用 ε" role="presentation">ε 表示，且取值为10−3。

由此，我们看到ADMM算法可以很好地将电网运营商的信息和用户信息分离并进行求解，这不仅可以避免隐私信息泄露问题，同时该算法较文献 [10] 提出的DOA算法在性能上表现良好，这将在结果分析中具体说明。算法过程具体如下：

步骤1：对于每个用户i，初始化参数。迭代次数k = 0，更新用电量 p^i(0)∈p" role="presentation">p^i(0)∈p，前时刻的最优用电量 pi∗(0),pi∗(−1)∈p" role="presentation">pi∗(0),pi∗(−1)∈p，总用电量 g0" role="presentation">g0 及拉格朗日对偶变量 λ0∈(0,1)" role="presentation">λ0∈(0,1)，权衡参数 α" role="presentation">α，罚参数 ρ" role="presentation">ρ 和阈值 ε" role="presentation">ε。

步骤2：式(15)子优化问题进行交替计算。由第k步的 gk" role="presentation">gk，根据式(15)中的第一个子问题求解出用户的用电量 pik+1" role="presentation">pik+1，然后将该结果传递给电网运营商，并求解第二个优化子问题，并计算出 gk+1" role="presentation">gk+1，然后将此信息传送给供电商。

步骤3：收敛判断。当原始残差 γk+1" role="presentation">γk+1 和对偶残差 sk+1" role="presentation">sk+1 、均小于收敛阈值 ε" role="presentation">ε 时，算法终止计算，则步骤2得到的解即为最优解；否则，进行步骤4。

步骤4：更新增广拉格朗日对偶变量 λk+1" role="presentation">λk+1，令 k=k+1" role="presentation">k=k+1。

步骤5：更新式(15)的 p^i(t)" role="presentation">p^i(t)，返回步骤2，进行下步迭代过程。

5. 结果分析

在本节中，我们仿真数据和参数参考于南加州爱迪生(SCE)地区记录的数据 [12]。然后将文献 [10] 中的算法DOA和该算法进行比较，研究两者的性能优劣。

在本文中，我们认为对于一个小区域的用户数设为N = 20，在智能设备间交互信息的更新周期是每15分钟为一间隔，总时长为24小时。用户i的用电需求 p∈[1,3]" role="presentation">p∈[1,3]。供电成本函数中的参数设置 a=0.05" role="presentation">a=0.05， b=c=0" role="presentation">b=c=0 ；以及权衡参数 α=0.1" role="presentation">α=0.1。

在关于用户的用电量 p^i(t)" role="presentation">p^i(t) 收敛性比较，我们给出了两个用户进行比较，如图1、图2：

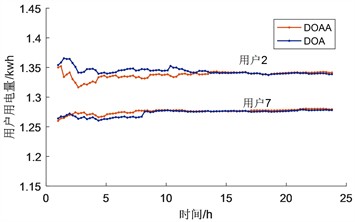
Figure 1. Comparison of the two algorithms for the power consumption p^i(t)" role="presentation">p^i(t) of different users

图1. 对于不同用户的用电量 p^i(t)" role="presentation">p^i(t) 两种算法的比较

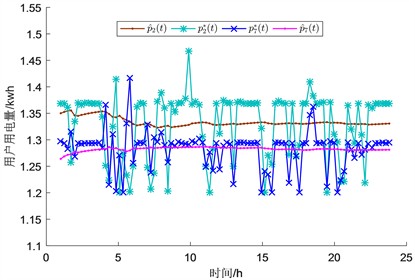
Figure 2. Power consumption p^i(t)" role="presentation">p^i(t) and optimal power consumption pi∗(t)" role="presentation">pi∗(t) of different users

图2. 不同用户的用电量 p^i(t)" role="presentation">p^i(t) 和最优用电量 pi∗( t )" role="presentation">pi∗( t )

从图1中我们可以看出来，DOA算法和DOAA算法在最后均逐渐收敛于定值 P¯i∗" role="presentation">P¯i∗，而收敛性能上算法DOA的表现不如DOAA，这是因为ADMM算法较DOA算法具有更好的收敛性能以及历史用电信息对后期电量的作用。另一方面，图中用户2和7之间的区别在于偏好参数 wi(t)" role="presentation">wi(t) 的选择，同时也验证了DOAA的可行性。这说明基于ADMM的分布在线算法既具备了文献 [9] 避免隐私泄露的问题，也表现出较好的性能。图2表明分配用户的最优用电量的值是在实际用电量上下波动的，随着时间 T→∞" role="presentation">T→∞，最终会逐渐收敛到实际用电量值。

另外，我们也对电网负载控制上也做出了相应地比较，这主要通过总量用电来体现，具体如图3：

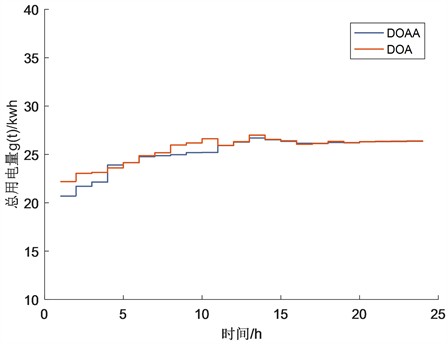
Figure 3. Comparison of the two algorithms on smooth grid load

图3. 两个算法在平滑的电网负载上的比较

从图3中，可以看到两个算法在平滑电网负载上，DOAA的表现较DOA更为好些，主要是因为DOAA把前两次用电历史的结果作为下一时间开始的一个影响因子，这为供电商在供电上提供很好的根据，由图3可以看出该算法在此约束下能更好地降低供电峰值。

6. 结语

在本文中，我们在相关算法的基础上，为满足分离变量达到减少隐私信息泄露的问题，同时我们也调整了约束条件，使得在电力调度中历史信息作为下一时间的一个影响因子，以此来提高性能，所以我们提出基于ADMM的分布式在线算法，并在文中与DOA算法作了对比。通过数值实验可知该算法具有较好的收敛性能，同时在平滑电网负载上也有较好的表现。与此同时也继承了DOA算法的优点：分离运营商与用户之间的敏感信息并分别进行求解，为有效地规避隐私泄露的问题作出很好的处理。未来将对智能电网场景中考虑多种因素并如何优化电力调度的相关问题进行更深入的研究，将会为智能电网的建设提供很好的参考。

NOTES

*通讯作者。

网址：基于ADMM的智能电网电力调度优化分布式在线算法 https://www.yuejiaxmz.com/news/view/274066

⬅️上一篇：【国网天津电力发布2022年电力

➡️下一篇：家用垃圾袋

基于ADMM的智能电网电力调度优化分布式在线算法

相关内容

随便看看

最新动态分享

热点动态分享

专题

推荐动态分享