分治法解决循环赛日程表安排问题(C++)

分治法解决循环赛日程表安排问题(C++)

题目：
设有n=2^k个选手要进行网球循环赛，要求设计一个满足以下要求的比赛日程表：
（1）每个选手必须与其他n-1个选手各赛一次；
（2）每个选手一天只能赛一次。
（3） 循环赛一共进行n-1天。
按此要求，可将比赛日程表设计成一个 n 行n-1列的二维表，其中，第 i 行第 j 列表示和第 i 个选手在第 j 天比赛的选手。

分析：
按分治策略，将所有的选手分为两半，n个选手的比赛日程表就可以通过为n/2个选手设计的比赛日程表来决定。递归地用对选手进行分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单。这时只要让这2个选手进行比赛就可以了。
然后再将右上角，右下角，左下角的内容扩展填入即可。

（黄色区域为输出的结果，第一列是参加比赛的队伍；从第二列开始是第 i 支队伍第 j 天和哪支队伍比赛）

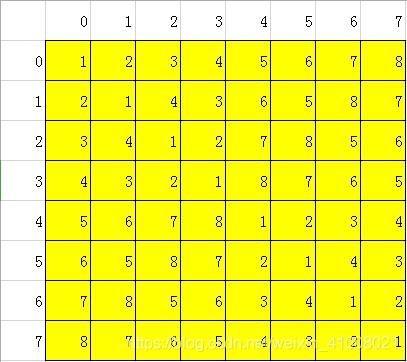
拓展
题目中只要求解决队伍个数为2^n的情况，但日常生活中并不总是那么凑巧的出现这种情况。
针对非2^n支队伍的情况，我才用的方法是将队伍数量凑为2的n次幂。再将与多出来的队伍比赛的日期设为轮空休息日。
（1）假如有7支队伍比赛，将队伍数凑成大于或等于7的最小的2的n次幂–8 。
（2）再按8支队伍，用分治法安排赛程。

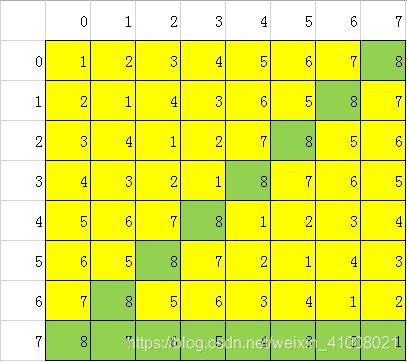
（3）再将 与多出来的队伍进行比赛的日期设为轮空休息日。

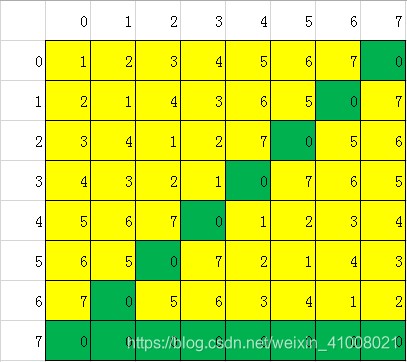
代码
函数功能介绍

void Divide(int n);//分治法赛程安排函数 int isTwoPower(int num);//判断是否为2的几次幂,返回值为大于或等于队伍数的最小的2的几次幂 12

完整代码

#include <iostream> using namespace std; int g[100][100];//存放赛程安排的数组 //赛程安排函数 void Divide(int n) {int i,j;int temp=2;g[0][0]=1;g[0][1]=2;g[1][0]=2;g[1][1]=1;while(temp!=n){//left lowerfor(i=temp;i<2*temp;i++)for(j=0;j<temp;j++)g[i][j]=g[i-temp][j]+temp;//right lowerfor(i=temp;i<2*temp;i++)for(j=temp;j<2*temp;j++)g[i][j]=g[i-temp][j-temp];//upper rightfor(i=0;i<temp;i++)for(j=temp;j<2*temp;j++)g[i][j]=g[i+temp][j-temp];temp=temp*2;} } //返回大于或等于num的最小2的几次方 int isTwoPower(int num) { int s=1; while(s<num) s=s*2; return s; } int main() { int num,i,j;//num为队伍数 int f;//存放大于或等于num的最小2的几次方 cout<<"Input the number of teams:"; cin>>num; f=isTwoPower(num); Divide(f);//将轮空那天标记为零if(f>num)for(i=0;i<num;i++)for(j=0;j<f;j++)if(g[i][j]>num)g[i][j]=0;//输出结果cout<<"The Schedule:"<<endl;for(i=0;i<num;i++){for(j=0;j<f;j++)cout<<g[i][j]<<" ";cout<<endl; }return 0; }

运行结果
(1)队伍数为2的几次幂的情况

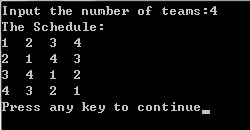
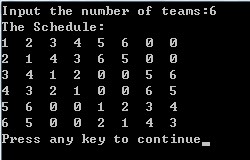
(2)队伍数为非2的几次幂的情况

靴靴大家观看，个人笔记，如有不严谨或错误，多谢指正~