动态规划

掌握决策模型如决策树、线性规划和动态规划 #生活技巧# #领导力技巧# #决策科学#

给定n个矩阵{A1,A2,…,An}，其中Ai与Ai+1是可乘的，i=1,2,…,n-1。考察这n个矩阵的连乘积A1A2…An。由于矩阵乘法满足结合律，故计算矩阵的连乘积可以有许多不同的计算次序，这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，则可以依此次序反复调用2个矩阵相乘的标准算法（有改进的方法，这里不考虑）计算出矩阵连乘积。若A是一个p×q矩阵，B是一个q×r矩阵，则计算其乘积C=AB的标准算法中，需要进行pqr次数乘。

例如，如果我们有四个矩阵A，B，C和D，我们将有：
（ABC）D =（AB）（CD）= A（BCD）= ....
不同组合得到的运算次数是不同的，例如A为 10 × 30 , B为 30 × 5 , C 为 5 × 60 那么

(AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 次运算 A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 次运算12

很明显第一种运算更为高效。
问题：给定一个数组P[]表示矩阵的链，使得第i个矩阵Ai 的维数为 p[i-1] x p[i].。我们需要写一个函数MatrixChainOrder（）返回这个矩阵连相乘最小的运算次数。
示例：

输入：P [] = {40，20，30，10，30} 输出：26000 有4个矩阵维数为 40X20，20X30，30×10和10X30。 运算次数最少的计算方式为： （A（BC））D - > 20 * 30 * 10 +40 * 20 * 10 +40 * 10 * 输入：P[] = {10，20，30，40，30} 输出：30000 有4个矩阵维数为 10×20，20X30，30X40和40X30。 运算次数最少的计算方式为： （（AB）C）D - > 10 * 20 * 30 +10 * 30 * 40 +10 * 40 * 3012345678910

1）最优子结构：
一个简单的解决办法是把括号放在所有可能的地方，计算每个位置的成本，并返回最小值。对于一个长度为n的链，我们有n-1种方法放置第一组括号。
例如，如果给定的链是4个矩阵。让矩阵连为ABCD，则有3种方式放第一组括号：A（BCD），（AB）CD和（ABC）D。
所以，当我们把一组括号，我们把问题分解成更小的尺寸的子问题。因此，这个问题具有最优子结构性质，可以使用递归容易解决。
2）重叠子问题
以下是递归的实现，只需用到上面的最优子结构性质。

//直接的递归解决 #include<stdio.h> #include<limits.h> //矩阵 Ai 的维数为 p[i-1] x p[i] ( i = 1..n ) int MatrixChainOrder(int p[], int i, int j) { if(i == j) return 0; int k; int min = INT_MAX; int count; // 在第一个和最后一个矩阵直接放置括号 //递归计算每个括号，并返回最小的值 for (k = i; k <j; k++) { count = MatrixChainOrder(p, i, k) + MatrixChainOrder(p, k+1, j) + p[i-1]*p[k]*p[j]; if (count < min) min = count; } return min; } // 测试 int main() { int arr[] = {1, 2, 3, 4, 3}; int n = sizeof(arr)/sizeof(arr[0]); printf("Minimum number of multiplications is %d ", MatrixChainOrder(arr, 1, n-1)); getchar(); return 0; }

123456789101112131415161718192021222324252627282930313233

上面直接的递归方法的复杂性是指数级。当然可以用记忆化存储优化。应当指出的是，上述函数反复计算相同的子问题。请参阅下面的递归树的大小4的矩阵链。函数MatrixChainOrder（3，4）被调用两次。我们可以看到，有许多子问题被多次调用。

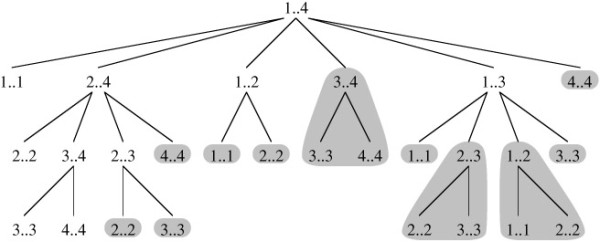
动态规划解决方案
以下是C / C + +实现，使用动态规划矩阵链乘法问题。

#include<stdio.h> #include<limits.h> int MatrixChainOrder(int p[], int n) { /* 第0行第0列其实没用到 */ int m[n][n]; int i, j, k, L, q; //单个矩阵相乘，所需数乘次数为0 for (i = 1; i < n; i++) m[i][i] = 0; //以下两个循环是关键之一，以6个矩阵为例(为描述方便，m[i][j]用ij代替) //需按照如下次序计算 //01 12 23 34 45 //02 13 24 35 //03 14 25 //04 15 //05 //下面行的计算结果将会直接用到上面的结果。例如要计算14，就会用到12，24；或者13，34等等 for (L=2; L<n; L++) { for (i=1; i<=n-L+1; i++) { j = i+L-1; m[i][j] = INT_MAX; for (k=i; k<=j-1; k++) { q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if (q < m[i][j]) m[i][j] = q; } } } return m[1][n-1]; } int main() { int arr[] = {1, 2, 3, 4}; int size = sizeof(arr)/sizeof(arr[0]); printf("Minimum number of multiplications is %d ", MatrixChainOrder(arr, size)); getchar(); return 0; } 时间复杂度: O(n^3) 空间复杂度: O(n^2)

123456789101112131415161718192021222324252627282930313233343536373839404142434445

参考：http://www.geeksforgeeks.org/dynamic-programming-set-8-matrix-chain-multiplication/
转载：http://www.geeksforgeeks.org/dynamic-programming-set-8-matrix-chain-multiplication/

网址：动态规划 https://www.yuejiaxmz.com/news/view/429768

相关内容

动态规划的应用
动态规划之0
递归和动态规划（python)
算法动态规划01背包问题
动态规划算法在生活中的应用
动态规划在实际生活中的应用
动态规划之最大子段和问题
动态规划问题dp问题以及经典问题
旅行商问题（动态规划方法，超级详细的）
动态规划思想的实际应用

随便看看