R入门（四）

R语言统计分析：生物信息学或数据分析入门 #生活技巧# #工作学习技巧# #编程语言学习路径#

文章目录 今日版块==循环==循环的魅力---> ==动画==这一节叫做超越循环,how?? apply()家族的小秘密拓展==>==提示进度==

今日版块循环

大面积展示作业

#作业5.1打印出奇数 for (i in 1:100) { if(i %% 2 == 1){ print(i) } } #5.1参考答案 for(i in seq(from=1,to = 100,by = 2)) print(i) #或者 print(seq(from=1,to = 2,by = 100)) 12345678910

关于马尔萨斯人口增长模型的R实现,设定增长率,初始年人口数,增长年数

#人口的马尔萨斯增长模型 r <- 0.011 x <- numeric(100) x[1] <- 66.8 for (i in 2:100) { x[i] <- x[i-1]*r+x[i-1] } #画出增长模型 y <- seq(from=2008,length.out = 100,by = 1) plot(y,x) #找到人口在哪一年开始超过100亿 abline(h = 100,col='darkgreen',lty=2) locator(1) #结果显示大概是在2045年人口超过100亿 $`x` [1] 2044.262 $y [1] 100.0087

1234567891011121314151617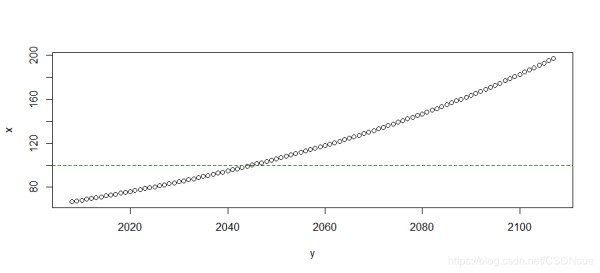

按要求生成矩阵m,m中的元素根据矩阵 x , y x,y x,y而来, m [ i , j ] = x [ i ] ∗ y [ j ] m[i,j]= x[i]*y[j] m[i,j]=x[i]∗y[j]

#作业5.2 #马尔萨斯增长模型中,x为向量,用0来占位, #在本作业中,m为矩阵,用NA来占位,先设置好框架,几行几列,再往里面填数 example("matrix") x <- c(2,3,5) y <- c(1,2,3,4) m <- matrix(nrow = length(x),ncol = length(y)) for (i in 1:length(x)) { for (j in 1:length(y)) { m[i,j] <- x[i]*y[j] } } #image()绘制的是颜色网格图 example("image") 1234567891011121314

总结:
1.当要设定某长度的向量,或某维度的矩阵时,要用占位符,进行占位,把框架搭建好。

其中，向量是用0来占位，numeric(长度) [见马尔萨斯增长模型];矩阵用NA来占位,搭建框架matrix(nrow=a,ncol=b) [见]作业5.2

2.如果是两个循环变动的变量,需要循环套循环,for()语句套for()语句,

通俗来讲,就是固定外圈for的某个值,内圈for走一遍,再换个外圈for(),内圈for()所有数值再走一遍

循环的魅力—> 动画

康威生命游戏的R实现

规则:

每个玩家有一个国际象棋棋盘，除了边缘外，每个方格被8个方格包围。每个方格里可以居住一个细胞，假定每个细胞周边养活细胞的资源是有限的。游戏开始时，由玩家选任意多个方格，每个方格放进去一个活细胞。在下一个时刻，细胞的生死由相邻8个方格中的活细胞数量决定：==>当相邻的活细胞多于3时，那么由于僧多粥少，中央的这个细胞就会饿死；当相邻的活细胞少于2时，中央这个细胞会因太孤单而死只有在相邻活细胞数量刚好是2或3时，中央的细胞才会活下去;这种情况下，即使中央原本没有细胞，也会诞生一个新细胞。

install.packages('simecol') require(simecol) # 40 * 40的棋盘: m <- matrix(0, 40, 40) # 玩家放置细胞的初始条件。0 表示该位置没有细胞，1 表示有细胞： m[5:35, 19:21] <- 1 # 白色表示没有细胞，绿色有细胞： image(m, col = c("white", "darkgreen"), axes = FALSE) for(i in 1:200) { nn <- eightneighbours(m) m.old <- m # 当周围有三个细胞时该位置产生细胞： m[m.old == 0 & nn == 3] <- 1 # 当周围细胞少于 2 个（太孤单）或大于 3 个（太拥挤）时， # 该位置细胞死亡。 m[m.old == 1 & (nn < 2 | nn > 3)] <- 0 image(m, col = c("white", "darkgreen"), axes = FALSE) Sys.sleep(0.1) }

12345678910111213141516171819

注释:

simecol() 扩展包是用来使用eightneighbours()函数,作用类似于windows扫雷游戏中,每个方格的数字表示周围8个方格地雷数量之和,这个函数就是计算矩阵的每个元素相邻周围8个元素之和。其中调用包使用require(),而不是library(),好生奇怪,为啥?这个代码没有看明白,还需深究

png(paste("F:/R lab/学R/data/conway_", formatC(i,width = 2,flag = '0'),'.png', sep = ''), width = 300,height = 300) image(m,col = c('white','darkgreen'),axes=FALSE) dev.off() 1234567

将连续图片连接的软件ffmpeg
ffmpeg: https://ffmpeg.org/
注释:

保存图片,在作图前后增加打开和关闭图片的函数,像上述代码存成的png格式照片那样但是运行出来,路径下只有最后一张图片。ffmpeg软件下载了,但是不知道怎么用,英文网站看不懂,OMG!

R制作的3D立体动画

install.packages('rgl') require(rgl) example(movie3d) 123 这一节叫做超越循环,how??

wp <- as.data.frame(WorldPhones) #将WorldPhones转化为数据框数据 wp$year <- as.numeric(rownames(wp)) #将行名称转为数值型数据 #将数据格式重新调整为3列的数据框,三列分别是电话数量,年份,洲名 mydata3 <- data.frame( nphone = unlist(wp[,1:7]), year = rep(wp$year, 7), conti = rep(names(wp)[1:7], each = nrow(wp))) summary(mydata3) str(mydata3) mydata3$year <- as.factor(mydata3$year) #转为因子格式 nlevels(mydata3$year) levels(mydata3 $ year) 1234567891011

#练习5.4 boxplot(nphone~year, data = mydata3, col= rainbow(6)) 12

*[花里胡哨的图片就不演示了]* 1

注释:

str()函数可以用来看数据结构将数值型数据转为因子型数据,as.factor()，查看因子个数nlevels()，查看因子水平情况levels()因子的含义就是分类的意思

根据因子这一结构,做一下展示,比如对不同年份计算几大洲的电话总和

方法一：for（）循环大法

for (i in levels(mydata3$year)) { print(sum(mydata3$nphone[mydata3$year == i])) } 123

方法二：apply（）函数大法

tapply(mydata3$nphone, mydata3$year, sum) 1

注释： tapply（），（table apply的缩写），根据年份，对nphone求和，优秀！！！

apply()家族的小秘密

apply家族：
apply（），tapply（），lapply（），sapply（），rapply（），vapply（），mapply（）

myfile1 <- file.choose() myfile1 mydata2 <- read.csv(file = "F:\\R lab\\学R\\r4r\\co2.csv") smr1 <- summary(mydata2) 1234

注释: summary() 得到的是一个列表,存储的是字符型信息,无法对其进行数字运算操作，若想对其操作，可以用lapply（）函数，lapply（）返回的是列表。sapply（）返回的是数据框。

> smr2 <- lapply(mydata2,summary) > smr2[[2]][6]-smr2[[2]][1] Max. 47.81 > smr3 <- sapply(mydata2,summary) > smr3[6,2]-smr3[1,2] [1] 47.81 1234567

plot() 的第五种化身——箱线图

当plot（）中的x为分类型变量时，会自动转化为箱线图

plot(x = mydata3$year, y = mydata3$nphone) #等同于 boxplot(mydata3$nphone~mydata3$year) 123

#作业5.5 tapply(mydata3$nphone, mydata3$conti, max ) tapply(mydata3$nphone, mydata3$conti, min ) tapply(mydata3$nphone, mydata3$conti, median ) 1234 拓展==>提示进度 提示进度，函数WinDialog(),或者print()函数当命令执行完毕后，点击"ok"，便进行下一个操作WinDialog()和file.choose()一样属于与用户交互对话的函数

N <- numeric(100) N[1] <- 66.8 r <- 0.011 for (t in 1:3) { N[t+1] <- N[t] + r * N[t] winDialog(type = c('ok'), message = paste('population in',t + 2007, 'will be', N[t+1])) } 123456789 马尔萨斯人口模型，交互式自动选择年份，反馈出人口预测数
从弹出的窗口选择年份，自动给出结果

r <- 0.011 N <- numeric(100) N[1] <- 66.8 for (i in 2:100) { N[i] <- N[i-1]*r+N[i-1] } n <- winDialogString( message = 'which yearis population would you like to see', default = '2050') winDialog(type = c('ok'),message = paste( 'population in', n ,'will be',N[as.numeric(n)-2007])) 1234567891011

网址：R入门（四） https://www.yuejiaxmz.com/news/view/477230

相关内容

设jr}本=h1+)+c,则r四d=（
【精品】r;点P在圆上d=r;点P在圆内d95
日立R
【佳能EOS R 单机】报价
根据城市用地和城市人口增长速度的差值（R）,将其分为土地扩张型（R>0）、人口增长型（R＜0）、人地协调型（R=0）和人地收缩型（人口和用地规模缩减）四类
R(A+B)＜=R(A)+R(B): R(AB)＜=min(R(A)+R(B)): A为m×n矩阵,r（A）＝n,则AX＝0只有零解。设矩阵A为m×n的秩R（A）=m；Ax=b 有解；
【佳能EOS R套机 RF 24
废旧塑料回收与再生入门 书籍下载
利用Win+R命令清理垃圾文件的有效方法（通过快捷方式Win+R清理垃圾文件）
若A为n阶方阵，r(A)=r，则矩阵A中存在r个列向量线性无关． 若r...

随便看看