[题目]如图.⊙O是△ABC的外接圆.点O在BC边上.∠BAC的平分线交⊙O于点D.连接BD.CD.过点D作BC的平行线与AC的延长线相交于点P．(1)求证:PD是⊙O的切线,(2)求证:△ABD∽△DCP,(3)当AB=5cm.AC=12cm时.求线段PC的长．题目和参考答案——青夏教育精英家教网——

发布时间：2025-05-05 16:38

热线号码是家长教育问题的求助途径 #生活技巧# #家庭教育建议# #家庭教育热线#

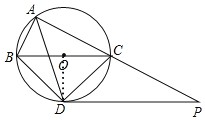
【题目】如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．

（1）求证：PD是⊙O的切线；

（2）求证：△ABD∽△DCP；

（3）当AB=5cm，AC=12cm时，求线段PC的长．

试题答案在线课程

【答案】（1）证明见解析；（2）证明见解析；（3）CP=16.9cm．

【解析】（1）先判断出∠BAC=2∠BAD，进而判断出∠BOD=∠BAC=90°，得出PD⊥OD即可得出结论；

（2）先判断出∠ADB=∠P，再判断出∠DCP=∠ABD，即可得出结论；

（3）先求出BC，再判断出BD=CD，利用勾股定理求出BC=BD=，最后用△ABD∽△DCP得出比例式求解即可得出结论．

（1）如图，连接OD，

∵BC是⊙O的直径，

∴∠BAC=90°，

∵AD平分∠BAC，

∴∠BAC=2∠BAD，

∵∠BOD=2∠BAD，

∴∠BOD=∠BAC=90°，

∵DP∥BC，

∴∠ODP=∠BOD=90°，

∴PD⊥OD，

∵OD是⊙O半径，

∴PD是⊙O的切线；

（2）∵PD∥BC，

∴∠ACB=∠P，

∵∠ACB=∠ADB，

∴∠ADB=∠P，

∵∠ABD+∠ACD=180°，∠ACD+∠DCP=180°，

∴∠DCP=∠ABD，

∴△ABD∽△DCP；

（3）∵BC是⊙O的直径，

∴∠BDC=∠BAC=90°，

在Rt△ABC中，BC==13cm，

∵AD平分∠BAC，

∴∠BAD=∠CAD，

∴∠BOD=∠COD，

∴BD=CD，

在Rt△BCD中，BD2+CD2=BC2，

∴BD=CD=BC=，

∵△ABD∽△DCP，

∴，

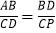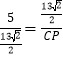∴CP=16.9cm．

练习册系列答案

年级高中课程年级初中课程高一高一免费课程推荐！初一初一免费课程推荐！高二高二免费课程推荐！初二初二免费课程推荐！高三高三免费课程推荐！初三初三免费课程推荐！

更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学来源：题型：

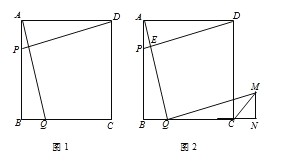
【题目】如图1，在四边形ABCD中，AB=BC=CD=AD=4cm，∠BAD=∠B=∠C=∠ADC=90°，点P以1cm/s的速度自点A向终点B运动，点Q同时以1cm/s的速度自点B向终点C运动，连接AQ、DP，设运动时间为t s．

（1）当t=　　s时，点P到达点B；

（2）求证：在运动过程中，△ABQ≌△DAP始终成立；

（3）如图2，作QM∥PD，且QM=PD，作MN⊥射线BC于点N，连接CM，请问在Q的运动过程中，∠MCN的度数是否改变？如果不变，请求出∠MCN；如果改变，请说明理由．

查看答案和解析>>

科目：初中数学来源：题型：

【题目】将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

（1）求证：CF∥AB．

（2）求∠DFC的度数．

查看答案和解析>>

科目：初中数学来源：题型：

【题目】（8分）如图，一艘轮船以15海里/时的速度，由南向北航行，在A出测得小岛P在北偏西方向上，两小时后，轮船在B处测得小岛P在北偏西30°方向上．在小岛周围18海里内有暗礁，若轮船

不改变方向仍继续向前航行，问：有无触礁的危险？说明你的理由．

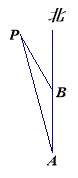
查看答案和解析>>

科目：初中数学来源：题型：

【题目】某网店销售甲、乙两种羽毛球，已知甲种羽毛球每筒的售价比乙种羽毛球多15元，王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球，共花费255元．

（1）该网店甲、乙两种羽毛球每筒的售价各是多少元？

（2）根据消费者需求，该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒，且甲种羽毛球的数量大于乙种羽毛球数量的，已知甲种羽毛球每筒的进价为50元，乙种羽毛球每筒的进价为40元．

①若设购进甲种羽毛球m筒，则该网店有哪几种进货方案？

②若所购进羽毛球均可全部售出，请求出网店所获利润W（元）与甲种羽毛球进货量m（筒）之间的函数关系式，并说明当m为何值时所获利润最大？最大利润是多少？

查看答案和解析>>

科目：初中数学来源：题型：

【题目】解方程：(1)x2＋4x－1＝0；

(2)2(x－3)2＝x2－9；

(3)(x－3)(x－1)＝3.

查看答案和解析>>

科目：初中数学来源：题型：

【题目】成都市民打车出行常用交通工具为出租车和滴滴快车．该市两种车的收费标准如下：

出租车：2千米以内9元；超过2千米的部分：2元/千米．

滴滴快车：里程费：1.6元/千米；时长费：18元/小时；远途费：0.8元/千米．(注：滴滴快车的收费由里程费、时长费、远途费三部分组成，其中里程费按行车的实际里程计算；时长费按照行车的实际时间计算；远途费的收取方式为：行车不超过8千米，不收远途费，超过8千米的，超过部分每千米加收0.8元)．假设打车的平均速度为30千米/小时．

（1）小明家到学校4千米，乘坐出租车需要多少元？

（2）设乘车路程为x(x＞2)千米，分别写出出租车和滴滴快车的应收费用(用含x的代数式表示)；

（3）小方和爸爸从家去环球中心(家到环球中心的距离天于2千米)，乘坐滴滴快车比乘坐出租车节约2.4元，求小方家到环球中心的距离．

查看答案和解析>>

科目：初中数学来源：题型：

【题目】如图，要设计一幅长为3xcm，宽为2ycm的长方形图案，其中有两横两竖的彩条，横彩条的宽度为acm，竖彩条的宽度为bcm，问空白区域的面积是_____．