电动汽车中基于T

电动汽车产生的噪音较小，有助于环保 #生活常识# #环保节能技巧# #电动汽车#

2332-7782 (c) 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TTE.2016.2535411, IEEE

Transactions on Transportation Electrification

> IEEE TRANSACTIONS ON TRANSPORTATION ELECTRIFICATION, TTE-Reg-2015-11-0100 <

3

B. Mathematical model of regenerative charging

Once the control system receives a brake signal, the motor

operation should be changed from the normal driving mode into

the regenerative charging mode. The key of the method is to

regulate the charging voltage/current from motor to battery by

dominates the conduction time. First, turn off all the switches

and make a BLDC motor as a generator. The switches are then

controlled via a high frequency PWM signal. In this paper, for

easily regulating the regenerative voltage, single-switch

modulation mode is adopted, where the active switch in the

lower side is modulated in turn. Specifically speaking, turns

only one of the lower switches to be periodically PWM, and

keeps the other five switches off. For a whole electrical cycle of

the regenerative charging process, each switch is modulated

within 120 electrical degrees. Therefore, the vehicle’s kinetic

energy is converted into electrical energy, which avoids the

waste of energy, lengthen the life of batteries, and increase the

driving range. To design the control system, the mathematical

model during regenerative charging should be firstly acquired.

Generality, take phases A and B as an example to analysis the

mathematical model, the back EMF e

ab

becomes a voltage

source and S4 is periodically PWM and other switches are OFF.

The amplitude of e

ab

remains a constant when the vehicle speed

is fixed.

1) State-space model of the charging converter

To construct the state-space model of the charging converter,

the equivalent circuit topology is analyzed according the state

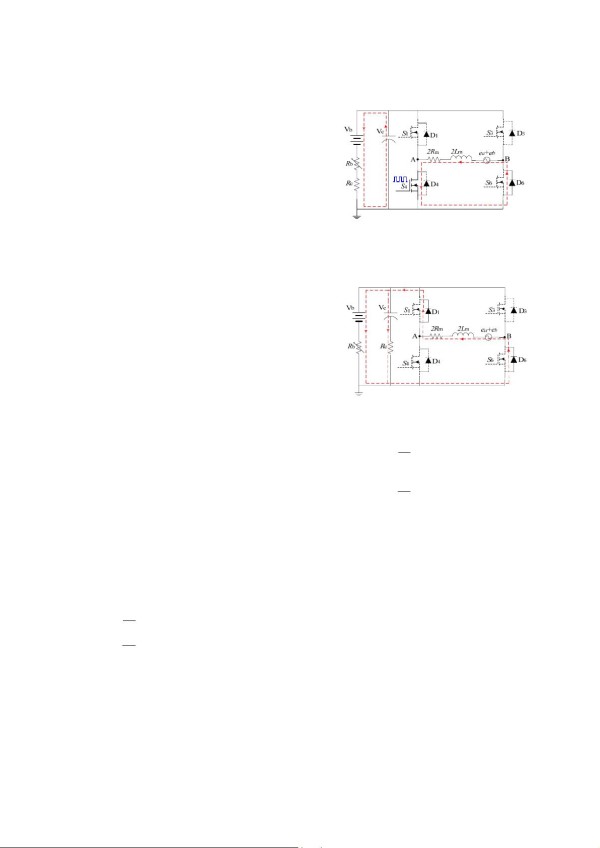
of S4 as following.

In a switching cycle T

s

, while S4 is turned on and others are

off, the armature inductance absorbs the released energy from

the back-EMF to pump up the terminal voltage of the armature.

The equivalent circuit of each commutation state is shown in

Fig.2, where the current i

L

flows through S4 and the

freewheeling diode D6. There are mainly two kinds of the EV

battery modeling approach. One is the electrochemical models

as in [25], which are widely used for battery design

optimization, heath characterization and control. The other is

the equivalent circuit models [26], which are primarily used for

online state-of-charge estimation and energy storage systems.

In this paper, a simplified equivalent circuit model is adopted as

in [2], which consists of a constant voltage source in series with

a variable resistance.

According to the principle of the KVL laws, the state

equations of the circuit in Fig. 2 are described as

S2_ON:

L

mmsdLab

11

c

cb

11

obccb

2(2 )

di

LRRRie

dt

dv

CRvRv

dt

VRRvRRv

−−

−−

⎧

=− + + +

⎪

⎪

⎪

=− +

⎨

⎪

⎪

=+

⎪

⎩

(2)

where d is the duty cycle, R

m

is the armature resistance, R

s

and

R

d

are the conduction resistances of the power switch and the

freewheeling diode, respectively; C and R

c

are the capacitance

and parasitic resistance of the dc-link capacitor, R

b

is the

equivalent load resistance of the battery, R= R

c

+R

b

; v

c

is the

voltage drop along the capacitor, v

b

is the battery voltage, V

o

is

the output charging voltage, and i

b

denotes the charging current.

−

−

+

c

i

b

i

+

L

i

Fig. 2. Equivalent circuit topology during S4 on (The red dotted line indexes

the current path.)

While the terminal voltage of the armature is high enough to

that of the battery, all the switches are turned off and the circuit

is equivalent to act as a non-isolated boost converter to charge

the battery as shown in Fig. 3.

−

−

+

c

i

b

i

+

L

i

Fig. 3. Equivalent circuit topology during S4 off (The red dotted line

indexes the current path)

Similarly, according to the principle of the KVL laws, the

state equations in Fig. 3 are described as

S2_ OFF:

1

L

mmdcbL

11

bccbab

11 1

c

bL c b

111

obcLbccb

2(22 )

di

LRRRRRi

dt

RR v RR v e

dv

C RRi Rv Rv

dt

V RRR i RR v RR v

−

−−

−− −

−−−

⎧

=++

⎪

⎪

++−

⎪

⎨

⎪

=−+

⎪

⎪

=++

⎩

(3)

2) Dynamic equivalent model of the charging converter

By selecting the state variables as x=[i

L

, v

c

]

T

and the output

as the charging voltage y=V

o

(t), the dynamic equations can be

transformed into the followings:

,

,

ON ON ab ON ON ON

OFF OFF ab OFF OFF OFF

ABegyC f

ABegyC f

=+ + =+

⎧

⎨

=+ + =+

⎩





xx x

xx x

(4)

where the coefficient matrices under S2_ON and S2_OFF are

1

2

0

0

ON

a

A

a

⎡

⎤

=

⎢

⎥

⎣

⎦

,

34

b

22

OFF

aa

A

Ra a

⎡

⎤

=

⎢

⎥

−

⎣

⎦

,

1

m

(2L )

0

ON OFF

BB

−

⎡

⎤

==

⎢

⎥

⎣

⎦

,

T

1

[0 ]

ON

g

g=

,

T

21b

[]

OFF

g

ggv=

,

1

b

[0 ]

ON

CRR

−

=

,

-1 -1

bc bOFF

CRRRRR

⎡

⎤

=

⎣

⎦

,

1

cbON OFF

f

fRRv

−

==

;

and the coefficients

1msdm

=(2 ++)/2aRRRL−

,

2

=1/aCR

−

,

3mdmcbm

=( +)/ /(2 )aRRLRRLR−−

,

4b m

=/(2 )aR LR

,

12b

=

g

av

−

,

2cmb

=/(2)

g

RLRv−

.

By multiplying both sides of the above equations by terms d

and d’=1-d, respectively, after average processing in state

网址：电动汽车中基于T https://www.yuejiaxmz.com/news/view/941313

相关内容

基于遗传算法的电动汽车有序充放电优化问题（附matlab源码）
基于数据驱动的电动汽车实时充电研究
浅谈基于峰谷电价的电动汽车有序充电策略
【电动车优化调度】基于模型预测控制(MPC)的凸优化算法的电动车优化调度附Matlab代码
【电车】基于 V2G 技术的电动汽车实时调度策略附Matlab代码
【充电站设计】电动汽车充电站设计规范 电动汽车充电站通用要求
电动汽车冬季行车难，有何省电技巧
十大热门纯电动汽车 电动汽车排名 最好的新能源纯电动车
电动汽车整车能耗影响因素分析
深度解读！电动汽车充电站设备安全防范要点

随便看看