基于大学生服装捐赠回收中的运输路线优化——以日照大学城为例

发布时间：2024-11-19 10:19

腰线的重要性：强调腰线可以优化身材比例，适合大多数女性穿着。 #生活知识# #生活美学# #服装搭配美学#

基于大学生服装捐赠回收中的运输路线优化——以日照大学城为例
Based on the Optimization Strategy of Transportation Route in College Students’ Clothing Donation and Recycling—A Case Study of Rizhao University Town

1. 引言

大学生是追求时尚的一个特殊群体，“新三年，旧三年，缝缝补补又三年”的时代已经远去。现在，大学生换“季”快，很多衣服还没穿几次就不喜欢了，而这种七八成新的衣服弃之可惜，留着又占用橱窗空间；再加上大学生的毕业季，也需要清理很多衣服，因此，旧衣回收箱应运而生。“旧衣回收”既可以避免了资源的浪费，又可以将衣服捐赠给贫困地区的孩子，实现资源的循环利用，最终获得双赢。本文以日照大学城为例进行分析，给出大学生闲置服装捐赠回收流程中的运输路线优化策略。

2. 日照大学城学生闲置服装捐赠回收现状

2.1. 闲置服装捐赠情况概述

“旧衣零抛弃”是“一三五”纺织行业发展循环的重点，提高服装的生命周期和利用率成为社会各界关注的重点。在旧衣物的处理方面，一般会通过三种方式：作为生活垃圾扔掉、进行二手交易、服装捐赠。由于我国目前还没有建立废旧衣物的分类处理制度，大多数的废旧衣物被作为垃圾扔掉，废旧衣物成为了固体垃圾中重大的组成部分。据统计，我国每年都会产生31亿件废旧衣物，但回收利用率不足10%。在服装捐赠方面，我国目前的服装捐赠以及回收利用还处于初步阶段，缺乏相关政策支持，回收力度和回收效率不高。近几年，在某些城市出现了服装回收捐赠箱，对废旧的服装进行回收捐赠处理。回收的衣物将有三种处理方式：一是将部分质量好的衣物捐赠给山区或者公益组织；二是将一些可穿性不高的衣物交给再生工厂，加工成农业、建筑和工业材料，或者用于纺织品生产；三是将少部分衣物出口到非洲等贫困国家，所得基金作为公基金。大学生是高消费群体，服装更新换代快，闲置衣物多，且大学生接受教育，衣物捐赠意识较高。本文以日照市大学城为例，探索闲置服装的捐赠以及回收处理情况。

2.2. 大学城捐赠情况调查分析

2.2.1. 调查方法

1) 实地调研

在日照市大学城内对各园区进行实地走访调研，通过观察法、询问法以及问卷调查法，了解大学生旧衣物捐赠以及衣物回收处理的情况。调研的主要内容包括大学生的衣物捐赠意识以及行动力高低、大学生服装捐赠的途径、衣物回收箱的工作人员的工作效率、回收箱衣物的去处等。调研的地点选取了文泽园、四季园、东升园、毓秀园、毓华园、德胜园。这几个园区居住着来自曲阜师范大学、济宁医学院、山东外国语学院等多所学校的学生。对调研地点进行实地走访采集资料，各个园区的衣物捐赠箱的数量为：文泽园4个、四季园3个、东升园4个、毓秀园4个、毓华园3个，德胜园2个。

2) 线上调查

先利用文献搜索法搜集有关衣服捐赠回收的知识，结合调研的主要内容，设计出符合日照大学城的调查问卷，调查的主要对象是在校学生，并通过预调查，对初稿进行修改，最后确定问卷的终稿 [1]，问卷内容见表1。

问卷问题

相关内容

被调查者的基本信息

性别；所在学校；所处年级；居住的园区

服装捐赠的意识

是否了解过服装捐赠与回收；学校是否有开展过服

装捐赠的公益活动；是否愿意将闲置的衣服捐出去

服装更换的频率

每季度是否会增添新衣服；一年大约淘汰多少件衣服；衣服

的平均寿命一般为多少；购买衣服时是否会考虑到所穿年限

闲置服装的处理

旧衣服被淘汰的原因；闲置衣服的处理方法

服装捐赠的认识与行动力

在园区内是否见到过服装捐赠回收箱；是否了解衣服捐赠箱内衣物的

去处；是否捐赠过衣服；闲置服装应如何进行处理才能有更高的利用率

Table 1. Contents of questionnaire

表1. 问卷内容

线上调查与线下调查相结合，在调查周期内，通过在日照大学城网络圈进行线上问卷调查，以及实地发放问卷，总共收回线上有效网络问卷265份，线下176份纸质问卷，总计回收441份有效问卷。

2.2.2. 调查数据分析

根据问卷及调查结果，利用调查的统计数据，将从被调查者服装更换的频率、闲置服装处理方式、几所大学不同年级男女学生闲置服装捐赠量的对比这几个方面进行分析。

1) 服装更换的频率

问卷中，对于学生服装更换的频率，以年为基本单位，从新衣的购买量和旧衣的淘汰量为研究内容，新衣的购买量有5件之内，5~10件，10~15件，15件以上四个选项，所得结果见图1。分析衣服的淘汰量，也划分为4个区间，分别为5件以内、5~10件、10~15件、15件以上，统计结果见图2。在新衣的购买量上，由图1中的数据显示，男生每年的购买量要少于女生。由图1和图2的统计结果对比可知，大学生整体的新衣购买量大于旧衣淘汰量，即每年都会出现一部分闲置衣服。

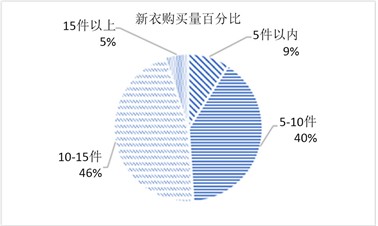
Figure 1. Percentage of new clothes purchased

图1. 新衣购买量百分比

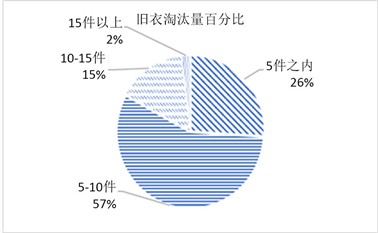
Figure 2. Percentage of obsolete clothes

图2. 旧衣淘汰量百分比

2) 闲置服装处理方式

根据调查，对于闲置服装的处理情况，分为4个选择，作为生活垃圾扔掉、进行二手交易、作为公益捐赠、送给身边的朋友、其他，数据统计结果见图3。由图3可以看出，在旧衣的处理上，作为生活垃圾扔掉仍然占很大部分，不过对于大学生而言，衣物捐赠意识较强，有30%的学生会将闲置的衣服进行捐赠。实地调研中了解到，有的大学内设有志愿者协会，每年都会发起衣服、图书等的公益捐赠，提高了学生服装捐赠的意识。

3) 男、女生服装捐赠量的对比

为了解性别以及学校对服装捐赠的影响，将收集到的有效问卷根据学校先进行初分类，再根据性别进行二次分类，以年为单位，统计出日照市大学城内不同大学的男、女生的人均服装捐赠数量，以此进行对比，统计结果见图4。由图4中的统计结果可以看出，女生的衣物捐赠量要大于男生，这与男生每年新增的衣服数量少于女生每年新增的衣服数量有关。不同学校的学生人均捐赠量有差异，这可能与每个学校学生接受的不同教育所致。据调查，被调查的78%的曲阜师范大学的学生表示学校有开展过衣物捐赠公益活动，则受其影响也会将闲置衣服捐赠到园区内的衣物回收箱内。

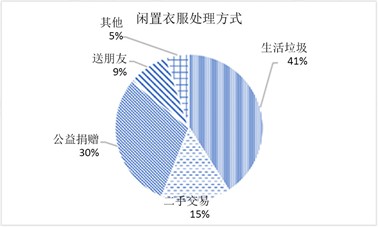
Figure 3. Disposal of idle clothes

图3. 闲置衣服处理方式

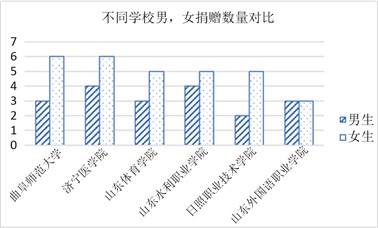
Figure 4. Comparison of donations of male and female in different schools

图4. 不同学校男、女捐赠数量对比

2.2.3. 闲置服装捐赠的特点

随着生活水平的提高，服装的更新换代越来越快，闲置服装的产生源地相对集中，服装的质量参差不齐，服装捐赠不同于一般的物品回收与捐赠，呈现出以下特点：

1) 集中性

相比其他的回收捐赠活动，服装的捐赠呈现出相对集中的特点，服装捐赠的开展一般会选择居民区、学校等地，在回收设置上有优势。

2) 价值非单调性

在服装回收的逆向物流过程中，由于会产生一系列运输、仓储等费用，会抵消部分回收的残余价值，呈现出价值递减性。但捐赠的服装，一般会有三种处理方法，一是将质量好的服装捐到山区或者公益组织；二是将一些可穿性不高的衣物交给再生工厂；三是将少部分衣物出口到非洲等贫困国家，所得基金作为公基金。回收的服装经过不同的处理之后，又会重新获得新的价值。

3) 时滞性

我国的服装捐赠回收还处于初步阶段，没有形成统一的标准，目前只是小范围开展了服装回收活动，且回收公司的回收效率有待提高。就园区、社区内设置的服装捐赠回收箱而言，工作人员会定时来回收，但是回收的周期较长，加上回收后的服装，还需要经过分类、储存、处理等环节，服装到达需要者需要经历较长的时间，这些决定了服装捐赠的时滞性。

4) 环保性

闲置的服装，如果直接扔进垃圾堆里或用于燃烧发电，则会对环境产生很大的危害，合成纤维、人造纤维留在地表面将可长达数千年之久，随着时间的推移，羊毛将不断产生甲烷，进而污染环境。但回收来的服装，一部分捐给需要的人，一部分送到再生工厂，提高了服装的利用率和价值，也减少了对环境的危害。

根据服装捐赠的这些特性，利用现代物流以及网络技术，进一步扩大服装捐赠的范围和影响面，提高服装捐赠的效率，并突破服装捐赠的路线规划、选址、库存优化，是目前研究的重点。

2.2.4. 捐赠回收后的运输情况

为拓宽旧衣捐赠的途径，日照市慈善总会与日照衣德环保科技有限公司、日照依旧爱环保科技有限公司两家公司合作，在居民小区设置旧衣回收箱，开展旧衣回收活动。目前，旧衣物回收箱是大学生捐赠服装的主要途径。他们将闲置服装洗干净后放入回收箱中，回收公司会每隔一段时间将回收箱内衣服运走，通常情况下是汽车运输。但是，由于回收箱设置范围广泛，运输路线复杂，由目前的一些数据来看，运输成本在回收总成本中仍占有较高的比例。若要降低服装回收的成本，我们可以从规划运输路线方面来入手，以运输成本最低为目标，通过建立模型来优化运输。日照大学城的旧衣回收路线见图5。

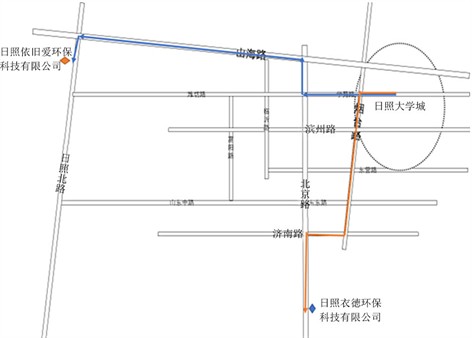
Figure 5. Recycling route of old clothes in university town

图5. 大学城旧衣物的回收路线

3. 研究意义

3.1. 对回收公司的效益

回收公司回收回来的衣服有两个去向：一是纯公益服务：将七八成新以上的衣服捐去贫困地区，这样，既有助于树立良好的企业形象，也能提高企业的社会亲和力，在无形中增强企业的竞争力。二是废物利用：对一些废弃衣服，企业可以变废为宝，实现服装的循环利用；或是将废弃服装溶解，重新作为原材料，绿色循环使用；或是将废弃服装制成拖把、抹布等降级利用。无论哪种方式，都可以节约成本，增加企业的效益。

3.2. 对消费者的效益

大学生通过捐赠旧衣，奉献爱心，能够弘扬奉献精神，提高他们的社会责任感，引导大学生在完成学业的同时成长为一个温暖有爱心的人。同时，也能在学校营造良好风气，使大学生关注公益事业，有助于大学生树立正确的价值观。另外，有些城市开展积分奖励活动，使爱心人士通过捐赠旧衣获得积分，利用积分兑换日用品，从而使捐赠者也能获得切实的好处。

3.3. 社会效益

1) 作为发展中大国，我们正面临着发展与资源匮乏之间的矛盾。走可持续发展之路，提高资源的利用能力迫在眉睫，而旧衣捐赠在一定程度上能够使资源循环再利用。旧衣捐赠是将衣服送给需要的人，能发挥出服装的最大效益；同时，它节约了资源，将无法穿着的废弃服装处理成其他产品，如制成拖把，使资源得到了再利用。

2) 奉献爱心，将衣服捐赠给困难的群众，使他们尽量减少购买衣服的支出，将钱花在更需要的地方，改善家庭生活质量。

3) 捐赠旧衣，可以减少焚烧旧衣物造成的环境污染，是打造绿色家园、低碳生活的重要途径。

4. 基于混合整数线性规划模型的闲置服装捐赠回收的运输路线优化

闲置服装种类繁多，且回收的服装的种类或损坏程度也不同，需采取对应的回收策略和再制造方式，因此产生了不同的逆向物流运输网络。对于闲置服装捐赠运输模型的建立以及方案的确定，其流程见图6。

针对于特定地区来说，每个地区都有相应已存在的运输节点，而且物流网络选择节点是逆向物流网络规划的重要方面 [2]。本文根据闲置捐赠服装的特征和逆向物流网络的特点，构造了独立性回收运输模型，然后建立了相应的混合整数线性规划(MILP)数学模型，并采用遗传算法模型进行求解。

4.1. 模型描述

独立性回收运输方式一般由专业第三方物流供应商实施运行。为了提高逆向物流系统的运行效率和效益，专业物流供应商需针对闲置捐赠服装单独建立回收运输网络。由于再制造不再依赖于原服装生产企业，而是由专业再制造商实施，因而可以按照区域进行规划，更加有利于逆向物流系统的运行。独立逆向物流运输结构由以下部分组成：大学城(消费区域)、再生材料市场、回收中心、再制造工厂、材料加工厂、捐赠中心以及废弃物处置中心。从消费区域收集来的闲置服装运送到回收中心，由回收中心对闲置服装进行检测、分类等处理，然后把可再制造的服装运送到再制造工厂，经过处理之后再运送到捐赠中心，可直接再重用服装经过简单的处理运送到捐赠中心，同时作为材料循环利用的运送到材料加工厂，不再利用的部分运送到废弃物处置中心。其中捐赠中心可包括低价的服装销售、再生材料销售和完全捐赠中心。

各部分的功能简介如下：

1) 消费区域：逆向运输网络的最底端，主要是收集点对闲置服装进行收集和存储。

2) 回收中心：主要对回收的服装进行检测、并根据不同质量和服装的种类进行分类和修补，同时具有一定的存储和配货功能。

3) 再制造工厂：主要对回收的服装进行再制造，从而使得服装具有新的使用价值，获得消费者和被捐赠者的喜爱，其工艺流程包括服装的拆解、清洗、翻新、更换和重新制作。

4) 材料加工厂、再生材料市场：主要对可循环的材料进行成分破解。

5) 捐赠中心：根据被捐赠者的需求进行配送。

6) 废弃物处置中心：主要是指服装的功能和材料等已经没有任何利用价值，且不能再进行经济处理，为了减少环境污染，送到指定的地点进行集中处理、焚烧或掩埋。

逆向运输网络设计的目标是在满足相关约束的条件下，确定各相关设施的位置和容量，从而得到合理的逆向运输网络，使某个地区的服装捐赠的期望收益达到最大。

4.2. 模型假设

1) 闲置服装回收运输网络中的消费区域的位置和数量是已知的；在单位时间内收集点的回收量和捐赠量是可预测的，且区域内闲置服装的回收量和服装拥有量成正比。

2) 回收中心的最大处理量与可预测的服装回收量有关，且再制造工厂、捐赠中心、废弃物处置中心的处理量只与检测中心的处理量相关，服装的再制造率和材料的回收率已知。

3) 已知各设施节点之间的运输成本和运输距离等，且在单位时间内闲置服装的运输成本已知，不受市场变化的影响，且只与运输量和、运输距离有关，不考虑设施建设和管理成本。

4) 不考虑在回收处理过程中的服装的损耗，即经检验合格的服装分为再制造服装和再利用服装，不合格的服装分为材料和废弃物。

5) 考虑闲置服装捐赠的特殊性，对企业所回收处理的服装给予一定的补贴。

4.3. 模型建立

1) 函数和约束条件

资料表明，在逆向物流系统中，运输成本约占整个系统运输成本的50%，因此，网络规划的成功与否，很大程度上取决于运输成本的大小。

运输成本：

β(q,d,v)=∑f=1F∑l=1Lqfl×dfl×vp×αfλ×αlλ+∑f=1F∑y=1Yqfy×dfy×vp×αfλ  +∑x=1X∑y=1Yqxy×dxy×vp+∑x=1X∑l=1Lqxl×dxl×αlλ×vp  +∑k=1K∑y=1Yqyk×dyk×vp+∑k=1K∑l=1Lqlk×dlk×αlλ×vp  +∑k=1K∑i=1IqkiM×dki×vp×αlλ+∑x=1X∑i=1IqixM×dix×αiλ×vp  +∑f=1F∑i=1IqifM×dif×vp×αfλ×αiλ+∑g=1G∑i=1IqigM×dki×vr×αgλ×αiλ" role="presentation">β(q,d,v)=∑f=1F∑l=1Lqfl×dfl×vp×αfλ×αlλ+∑f=1F∑y=1Yqfy×dfy×vp×αfλ +∑x=1X∑y=1Yqxy×dxy×vp+∑x=1X∑l=1Lqxl×dxl×αlλ×vp +∑k=1K∑y=1Yqyk×dyk×vp+∑k=1K∑l=1Lqlk×dlk×αlλ×vp +∑k=1K∑i=1IqkiM×dki×vp×αlλ+∑x=1X∑i=1IqixM×dix×αiλ×vp +∑f=1F∑i=1IqifM×dif×vp×αfλ×αiλ+∑g=1G∑i=1IqigM×dki×vr×αgλ×αiλ

 +∑z=1Z∑i=1IqizM×diz×vr×αiλ+∑f=1F∑s=1Sqfs×dfs×vr×αfλ×αsλ +∑x=1X∑s=1Sqxs×dxs×vr+∑f=1F∑z=1Zqfz×dfz×vr×αfλ +∑f=1F∑g=1GqfgM×dfg×vr×αfλ×αgλ+∑x=1X∑g=1GqxgM×dxg×vr×αgλ +∑x=1X∑z=1ZqxzM×dxz×vr+∑s=1S∑e=1EqseM×dse×vr×αsλ" role="presentation"> +∑z=1Z∑i=1IqizM×diz×vr×αiλ+∑f=1F∑s=1Sqfs×dfs×vr×αfλ×αsλ +∑x=1X∑s=1Sqxs×dxs×vr+∑f=1F∑z=1Zqfz×dfz×vr×αfλ +∑f=1F∑g=1GqfgM×dfg×vr×αfλ×αgλ+∑x=1X∑g=1GqxgM×dxg×vr×αgλ +∑x=1X∑z=1ZqxzM×dxz×vr+∑s=1S∑e=1EqseM×dse×vr×αsλ

约束条件：

1) 工厂、捐赠中心、检测中心、废弃物处置中心、再生市场等网络设施的处理量不大于其最大服务能力，如下列不等式。

2) 再制造工厂、捐赠中心、回收中心、材料加工厂的物流量守恒，如下列等式。

约束条件如下：

αfλ,αlλ,αiλ,αhλ,αgλ∈{0,1}" role="presentation">αfλ,αlλ,αiλ,αhλ,αgλ∈{0,1}

∑l=1L qfl+∑y=1Y qfy≤Af" role="presentation">∑l=1L qfl+∑y=1Y qfy≤Af

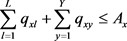
∑s=1S qse≤Ae" role="presentation">∑s=1S qse≤Ae

∑f=1F qfl+∑x=1X qxl≤Al" role="presentation">∑f=1F qfl+∑x=1X qxl≤Al

∑f=1F qfy+∑x=1X qxy≤Ay" role="presentation">∑f=1F qfy+∑x=1X qxy≤Ay

∑i=1I qigM+∑f=1F qfgM+∑x=1X qxgM≤Ag" role="presentation">∑i=1I qigM+∑f=1F qfgM+∑x=1X qxgM≤Ag

∑i=1I qixM+∑f=1F qfxM+∑x=1X qxzM≤Az" role="presentation">∑i=1I qixM+∑f=1F qfxM+∑x=1X qxzM≤Az

∑l=1L qlkM+∑y=1Y qyk≤Ak" role="presentation">∑l=1L qlkM+∑y=1Y qyk≤Ak

∑k=1K qlkM=∑f=1F qifM+∑g=1G qigM+∑x=1X qixM+∑z=1Z qixM" role="presentation">∑k=1K qlkM=∑f=1F qifM+∑g=1G qigM+∑x=1X qixM+∑z=1Z qixM

∑k=1K qlk=∑f=1F qfl+∑x=1X qxl" role="presentation">∑k=1K qlk=∑f=1F qfl+∑x=1X qxl

∑k=1K qyk=∑f=1F qfy+∑x=1X qxy" role="presentation">∑k=1K qyk=∑f=1F qfy+∑x=1X qxy

∑i=1I qifM=∑g=1G qfgM+∑z=1Z qfxM+∑e=1E qfz+∑y=1Y qfy+∑l=1L qfl" role="presentation">∑i=1I qifM=∑g=1G qfgM+∑z=1Z qfxM+∑e=1E qfz+∑y=1Y qfy+∑l=1L qfl

∑i=1I qixM=∑g=1G qxgM+∑z=1Z qxzM+∑e=1E qxs+∑y=1Y qxy+∑l=1L qxl" role="presentation">∑i=1I qixM=∑g=1G qxgM+∑z=1Z qxzM+∑e=1E qxs+∑y=1Y qxy+∑l=1L qxl

∑f=1F qfx+∑x=1X qxs=∑e=1E qse" role="presentation">∑f=1F qfx+∑x=1X qxs=∑e=1E qse

2) 符号说明见表2：

符号

表示含义

已开设工厂的地点

备选工厂的开设地点

备选捐赠中心的开设地点

已开设捐赠中心的地点

备选回收中心的开设地点

消费区域的地点

已存在废弃物处置中心的地点

备选废弃物处置中心的地点

备选材料加工厂的开设地点

再生材料市场的位置

由某一个地方到另一个地方的距离

某个流程环节上的服装的单位价格

某个设施中心最大的生产或处理能力

0~1变量，表示是否开设新的设施，是取1，否取0

由某个设施运往另一个设施中心的服装数量

Table 2. Symbol description

表2. 符号说明

4.4. 模型求解

在物流交通路径优化算法中，传统算法以遗传算法(GA)运用居多，遗传算法是计算数学中用于解决最佳化的搜索算法，是进化算法的一种 [3]，因此该模型求解利用遗传算法进行编码(编码工具：MATLAB)、选择、交叉和变异，再利用适应度函数进行评价 [4]，流程见图7。

4.5. 算例模拟

以日照大学城的数据进行上述模型模拟，针对每一个收集点，考察它应该归属哪个回收中心，收集点收集量是一定的，所以若构建一个逆向物流网络，从5个备选检测中心节点选3个作为检测中心。各检测中心的废弃率为0.15，再使用率为0.2，拆解率为0.32，在拆解中心，回收品拆解后的有用部件与拆解前的数量比为0.46。从3个备选捐赠中心节点选2个，从4个备选制造中心节点选2个作为再制造中心。有关数据见表3~8。

回收中心

回收品数量

Table 3. Recovery quantity of each recovery point (thousands)

表3. 各回收点的回收量(千件)

回收中心

检测中心

Table 4. Unit transportation cost from each recycling center to the testing center (1000 yuan/1000 pieces)

表4. 各回收中心到检测中心的单位运输成本(千元/千件)

检测中心

捐赠中心

Table 5. Unit transportation cost from each testing center to donation center (1000 yuan/1000 pieces)

表5. 各检测中心到捐赠中心的单位运输成本(千元/千件)

检测中心

再制造工厂

Table 6. Unit transportation cost from each testing center to remanufacturing factory (1000 yuan/1000 pieces)

表6. 从各检测中心到再制造工厂的单位运输成本(千元/千件)

检测中心

消费区域

Table 7. Unit transportation cost from testing center to consumption area (1000 yuan/1000 pieces)

表7. 从检测中心到消费区域的单位运输成本(千元/千件)

检测中心

废弃处置中心

Table 8. Unit transportation cost from each testing center to the waste disposal center

表8. 从各检测中心到废弃处置中心的单位运输成本

利用以上模型进行求解，结果如下：运输成本最低的方式为，检测中心为X3、X4、X5，再制造工厂为E2、E3，捐赠中心为L1、L3。

5. 评价与结论

通过针对日照市大学城服装捐赠情况的实地调研与相关资料分析，本文对大学城服装捐赠回收运输问题进行了分析，利用混合整数线性规划模型建立了基于运输成本最小原理的数学模型，并利用遗传算法进行了求解。算法模拟中对日照大学城的实例数据计算的结果表明，本文建立的数学模型科学、合理、可行，求解方法简便，有效解决了服装捐赠回收运输中减少成本的问题，对解决服装绿色和环境保护问题有重要参考价值 [5]。

致谢

首先，感谢蔡指导给我们的思路，以及撰写论文过程中提供的各种帮助；其次，感谢所有同学和朋友在调查阶段的帮忙，让我们顺利取得参考数据。

网址：基于大学生服装捐赠回收中的运输路线优化——以日照大学城为例 https://www.yuejiaxmz.com/news/view/134023

⬅️上一篇：“我有难，别人都帮我。我只要有钱

➡️下一篇：旧衣回收循环利用绿色环保变废为

基于大学生服装捐赠回收中的运输路线优化——以日照大学城为例

相关内容

随便看看

最新动态分享

热点动态分享

专题

推荐动态分享