浅谈*迭代加深*深度优先搜索

深度学习模型的超参数调优：网格搜索和随机搜索 #生活技巧# #学习技巧# #深度学习技巧#

目录

算法核心概念及思想

算法的产生

概念

拯救时间的函数

例题：《加法链》

如题，由于此文章只讲“迭代加深”，所以请先了解what “深度优先搜索” is。

算法核心概念及思想

算法的产生

如下一棵搜索树，它的最优解（符合要求且深度最小）在A2位置：

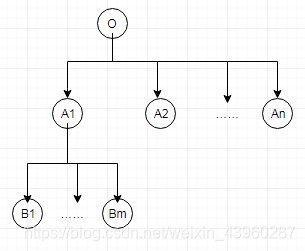
如果m、n都是大于106" role="presentation">106的数，那么使用深度优先搜索的话会在A1的子树下遍历超时，广度优先搜索会在存A1~An时耗掉过多空间。

既然要求深度最小的可行解，那么不妨每次用深度优先搜索搜深度≤k的节点，把k逐次增加，这样既可以最早搜到A2（判断A2可行后就直接返回了），又不会耗过多空间。于是，迭代加深搜索应运而生。

概念

迭代加深（Iterative deepening）搜索，实质上就是限定下界的深度优先搜索。即首先允许深度优先搜索K层搜索树，若没有发现可行解，再将K+1后重复以上步骤搜索，直到搜索到可行解。

在迭代加深搜索的算法中，连续的深度优先搜索被引入，每一个深度约束逐次加1，直到搜索到目标为止。

迭代加深搜索算法就是仿广度优先搜索的深度优先搜索。既能满足深度优先搜索的线性存储要求，又能保证发现一个最小深度的目标结点。

从实际应用来看，迭代加深搜索的效果比较好，并不比广度优先搜索慢很多，但是空间复杂度却与深度优先搜索相同，比广度优先搜索小很多，在一些层次遍历的题目中，迭代加深不失为一种好方法！

——来自某个专业的PPT

拯救时间的函数

由于迭代加深搜索是反复地使用深搜，要是深搜不剪枝的话会导致时间爆炸，所以根据迭代加深限定下界的特点，出现了乐观估计函数。

乐观估计函数是在迭代加深中的剪枝，其作用就是判断当前的搜索节点有无可能在限定下界中找出解。比如其中一种是估计当前要找到最优解最少需要多少步，如果当前深度加上这个步数大于了限定的下界，那么只好强制退出——等再一次扩宽下界时再搜这里。

例题：《加法链》

时间限制： 2秒      内存限制： 65536 KB

n的加法链是整数序列<a0，a1，a2，...，am>，具有以下四个属性：

a0 = 1am = na0 <a1 <a2 <... <am-1 <am对于每个k（1 <= k <= m），存在两个（不一定是不同的）整数i和j（0 <= i，j <= k-1），其中ak = ai + aj

你得到一个整数n。你的工作是为n构建一个最小长度的附加链。如果存在多个这样的序列，则任何一个都是可接受的。

例如，当要求输入5的加法链时，<1,2,3,5>和<1,2,4,5>都是有效的解决方案。

输入

输入将包含一个或多个测试用例。每个测试用例由一行包含一个整数n（1 <= n <= 100）组成。对于n，输入以零（0）的值终止。

输出

对于每个测试用例，打印一行包含所需的整数序列。将数字分隔一个空格。

 

样本输入

5 
7 
12 
15 
77 
0

样本输出

1 2 4 5 
1 2 4 6 7 
1 2 4 8 12 
1 2 4 5 10 15 
1 2 4 8 9 17 34 68 77

通过贪心的策略得知:   ∵a0&lt;a1&lt;a2&lt;...&lt;ak&#x2212;1" role="presentation">a0<a1<a2<...<ak−1，ak=ai+aj" role="presentation">ak=ai+aj（0≤i,j<k）

∴(ak)max=ak&#x2212;1+ak&#x2212;1=2&#x2217;ak&#x2212;1" role="presentation">(ak)max=ak−1+ak−1=2∗ak−1

所以让a每一项等于前一项的两倍，可以使数列增长最快。如果这样一个数列的第m项刚好大于等于n，那么可行解的长度一定大于等于m，否则不可能得到n。于是可以把下界从m开始加起，每次DFS搜一遍，最先搜出的一定最优。

此题的乐观估计函数也可以用这个数列来推断：从搜到的数出发，以增长最快的方式乘2一直推到下界位置，如果都小于n，那么此路继续搜下去一定无法在限界内得到n，就返回。

坑点：每次枚举前面的项时要倒着枚举。

#include<cstdio>

#include<cstring>

#include<iostream>

#include<algorithm>

using namespace std;

int n,k,l,a[105];

bool f;

void iddfs(int x){

if(x>l){

if(a[x-1]==n)f=1;

return;

}

for(int i=x-1;i>0;i--){

for(int j=i;j>0;j--){

if(a[i]+a[j]>a[x-1]&&a[i]+a[j]<=n&&!f){

a[x]=a[i]+a[j];

int s=a[x];

s<<=(l-x);

if(s<n)continue;

iddfs(x+1);

}

}

}

}

int main()

{

scanf("%d",&n);

while(n){

int s=1;

l=1;f=0;a[1]=1;

while(s<n)s<<=1,l++;

for(;!f;l++)

iddfs(2);/由于a1必为1，所以从a2搜起

for(int i=1;i<l;i++){

if(i-1)putchar(' ');

printf("%d",a[i]);

}

putchar('\n');

scanf("%d",&n);

}

return 0;

}

网址：浅谈*迭代加深*深度优先搜索 https://www.yuejiaxmz.com/news/view/318900

相关内容

开搜AI搜索深度分析报告
深度学习中的优化问题(Optimization)
谈信息搜索是现代生活最重要的技能之一
搭建社区服务平台：实战经验引领下的深度探索
“深”度保洁？笑谈“深度”的保洁真谛！
强化学习中的策略迭代算法优化研究
【ML4CO论文精读】基于深度强化学习的组合优化问题研究进展(李凯文, 2020)
SEO搜索优化方法
浅谈学习方式最优化.doc
现代人工作压力大，生活节奏快，中午的盒饭，深夜的夜宵 — 开搜AI免费问答搜索

随便看看