【机器学习】如何用Python书写计算任一多变量函数任一点的偏导导数值？

使用Excel计算平均值，选择数据后点击'公式'选项卡的'平均'函数 #生活知识# #生活经验# #软件#

摘要： 实际问题中主要涉及的还是多变量的函数，单一变量导数的计算其实是多变量导数求偏导的一个特例。本文将单变量求导的实现扩展到多变量求偏导，输出的结果不仅是各个变量的导数，也是函数在当前点的梯度。

关键词： 多变量，偏导，梯度

前言

上一篇文章【机器学习】如何用Python书写计算任一函数任一点的导数？，只介绍了单一变量的函数求导Python实现，而实际的问题中遇到大多都是多变量情况，但是知道偏导的概念后，再结合Python的特性就很容易解决如何用Python书写计算任一复合函数任一点的偏导导数值这个问题了。

1 偏导数

假设有以下函数：
f ( x 1 , x 2 ) = x 1 2 + 2 x 2 2 f(x_1, x_2) = x_1^2 + 2x_2^2 f(x1​,x2​)=x12​+2x22​
这也是为了便于介绍的，实际问题函数也比较复杂。这个函数已经有两个变量了。
使用Python实现如下：

def function_2(x): """一个多变量函数 y = x1^2 + 2*x2^2 x 可以为一个list或者tuple 元素要有两个以上 """ return x[0]**2 + 2*x[1]**2 12345'

本文所需要的依赖包如下：

import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D # 绘制3d图形 123'

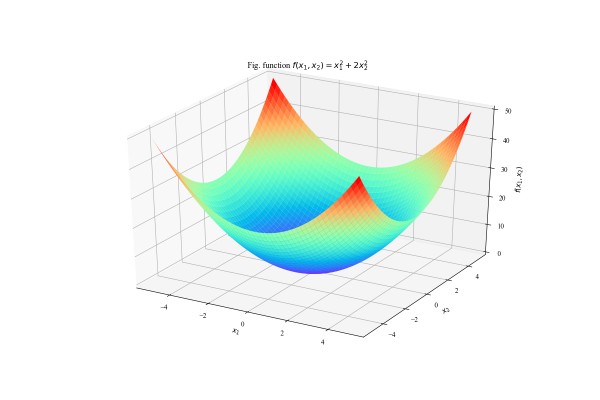
下面将这个函数可视化，看看是什么样子的。

绘图源码：

def plot_function_2(): """函数function_2 3维可视化 """ fig = plt.figure(figsize=(12, 8)) # 创建画板 ax = plt.axes(projection='3d') # 在当前画板上创建一个坐标轴 x1 = np.arange(-5, 5, 0.01) # 自变量1 x2 = np.arange(-5, 5, 0.01) # 自变量2 X1, X2 = np.meshgrid(x1, x2) # 将自变量坐标化 y = function_2([X1, X2]) # 计算对应左边的函数结果 ax.plot_surface(X1, X2, y, cmap='rainbow') # 绘制图形表面 ax.set_title("Fig. function $f(x_1, x_2)=x_1^2 + 2x_2^2$") ax.set_xlabel("$x_1$") ax.set_ylabel("$x_2$") ax.set_zlabel("$f(x_1, x_2)$") plt.show() # 显示 plot_function_2()

123456789101112131415161718

现在我们对目标函数中自变量x1和x2求偏导，需要注意的是当对x1求偏导的时候，我们把x2当作常数，对x2求导时也是如此把x1当作常数。其对应的导数如下：
∂ f ∂ x 1 = 2 x 1 , ∂ f ∂ x 2 = 4 x 2 \frac{\partial f}{\partial x_1}=2x_1, \quad \frac{\partial f}{\partial x_2}=4x_2 ∂x1​∂f​=2x1​,∂x2​∂f​=4x2​
实现对应的偏导数函数也比较简单如下：

def function_temp1(x): """f(x)对x1的偏导数 x x1的值 """ return 2*x def function_temp2(x): """f(x)对x2的偏导数 x x2的值 """ return 4*x 1234567891011'

2 偏导数Python实现

实现代码如下：

def numerical_diff(f, x): """ f为需要求导的函数 x为对应的变量 """ h = 1e-10 diff = np.zeros_like(x.size) for idx in range(x.size): tmp_val = x[idx] # 获取 # f(x + h) 的计算 x[idx] = tmp_val + h # 对于的需要计算偏导数变量的值略加一点 fxh1 = f(x) # 计算 # f(x-h)的计算 x[idx] = tmp_val - h # 对于的需要计算偏导数变量的值略减一点 fxh2 = f(x) diff[idx] = (fxh1 - fxh2)/(2*h) x[idx] = tmp_val # 还原值 return diff

123456789101112131415161718192021'

以点(2, 3)为例，比较自写求偏导的函数numerical_diff和标准函数计算的结果：

x = np.array([2., 3.]) print("numerical_diff result:\n") print(numerical_diff(function_2, x)) print("standard result:\n") print(np.array([function_temp1(x[0]), function_temp2(x[1])])) """ numerical_diff result: [ 4.00000033 12.00000099] standard result: [ 4. 12.] """ 1234567891011

从结果可以看出差别不是很大，基本上可以说是保持一致。

总结

numerical_diff函数的是有一定技巧的，我们需要注意的是在实际计算导数值时，与目标变量没有关系的部分，求导后都为0，与目标变量有关的部分会被进行差分求导的运算，补充一下求导是线性特征的，函数中的元素单独求导后再相加也是可以的。
硬核补充： numerical_diff函数输出的结果其实就是函数在某点的梯度。

网址：【机器学习】如何用Python书写计算任一多变量函数任一点的偏导导数值？ https://www.yuejiaxmz.com/news/view/433780

相关内容

Python随机函数等
使用python制作一个简单的任务管理器
Python函数
机器学习之数据预处理（Python 实现）
np.prod() 函数计算数组元素乘积等
Python数据分析：统计函数绘制简单图形
机器学习超参数优化算法（贝叶斯优化）
Python学习（一）
从零开始学 Python 之函数参数
Python小白的数学建模课

随便看看