大数据时代移动边缘计算架构中的差分隐私保护（一）

一些概念的学习

2019/3/17

以下资料整理来源于：本地化差分隐私：如何面对非可信的世界

随机响应技术就是主流的数据扰动机制，由于扰动添加的流程被分配到客户端，因此数据安全性的保证【不再依赖于一个可信实体】，降低了数据泄露的风险。通俗的说，本地化差分隐私就是让各个数据提供者根据一定的概率对自身数据加入噪声，而在数据聚合时，由于噪声符合一定的概率分布，因此不同记录间的噪声相互抵消，从而获得基于大样本的统计学特征。

论文 Erlingsson, Úlfar, Pihur V , Korolova A . RAPPOR: Randomized Aggregatable Privacy-Preserving Ordinal Response[J]. 2014. 中重点实现了ε=ln(p/(1-p))的ε-本地化差分隐私策略（不均匀的硬币）。

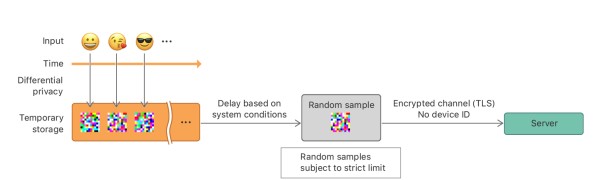
在WWDC2016会议上，苹果公司宣布了他们将差分隐私技术应用在iOS10，尽管没有开源相关技术，但是Learning with Privacy at Scale介绍了该技术实现的细节。如下图所示，在苹果对用户Emoji表情使用频数统计中，当一个Emoji表情使用事件发生时，首先对该事件使用ε-本地化差分隐私进行隐私化处理，然后将其暂存在设备上，在经过一定时间后，系统根据规则对暂存的数据随机抽样，并发送至服务器。

以下资料整理来源于：1. 差分隐私若干基本知识点介绍（一） 2. 差分隐私若干基本知识点介绍（二）

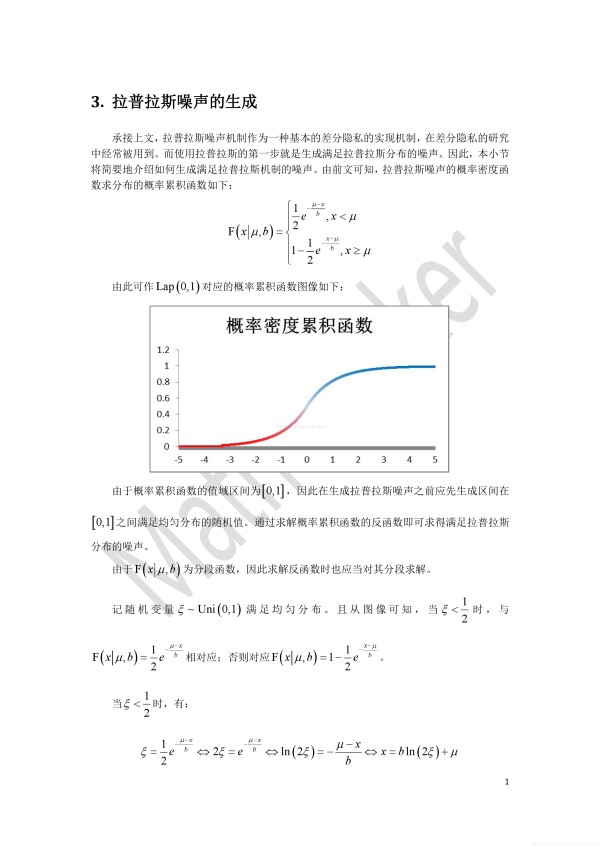
下面先给出Laplace分布实现代码：

import matplotlib.pyplot as plt import numpy as np def laplace_function(x,beta): result = (1/(2*beta)) * np.e**(-1*(np.abs(x)/beta)) return result #在-5到5之间等间隔的取10000个数 x = np.linspace(-5,5,10000) y1 = [laplace_function(x_,0.5) for x_ in x] y2 = [laplace_function(x_,1) for x_ in x] y3 = [laplace_function(x_,2) for x_ in x] plt.plot(x,y1,color='r',label='beta:0.5') plt.plot(x,y2,color='g',label='beta:1') plt.plot(x,y3,color='b',label='beta:2') plt.title("Laplace distribution") plt.legend() plt.show()

Laplace机制，即在操作函数结果中加入服从Laplace分布的噪声。

import numpy as np def noisyCount(sensitivety,epsilon): beta = sensitivety/epsilon u1 = np.random.random() u2 = np.random.random() if u1 <= 0.5: n_value = -beta*np.log(1.-u2) else: n_value = beta*np.log(u2) print(n_value) return n_value def laplace_mech(data,sensitivety,epsilon): for i in range(len(data)): data[i] += noisyCount(sensitivety,epsilon) return data if __name__ =='__main__': x = [1.,1.,0.] sensitivety = 1 epsilon = 1 data = laplace_mech(x,sensitivety,epsilon) for j in data: print(j)