机器学习
一个机器学习模型包含哪几个部件,谈谈您对每个部件的理解
特征提取部件:提取特征
损失函数部件:引导模型的优化方向
优化器部件:模型的优化,参数更新方法
评价指标:对模型性能的评估
softmax、交叉熵、正则函数
3.1 p ( y = 0 ∣ x ) = 1 1 + e − w x p(y=0 | x)=\frac{1}{1+e^{-wx}} p(y=0∣x)=1+e−wx1
p ( y = 1 ∣ x ) = e − w x 1 + e − w x \quad p(y=1 | x)=\frac{e^{-wx}}{1+e^{-wx}} p(y=1∣x)=1+e−wxe−wx
3.2 L ( y ^ , y ) = − 1 N ∑ i = 1 N ( y i l o g y ^ i + ( 1 − y i ) l o g ( 1 − y ^ i ) ) L(\hat y, y)=-\frac{1}{N} \sum_{i=1}^N (y_i log\hat y_i + (1-y_i)log(1-\hat y_i)) L(y^,y)=−N1∑i=1N(yilogy^i+(1−yi)log(1−y^i))
3.3 交叉熵损失函数求导 CSDN:https://blog.csdn.net/qq_40859461/article/details/89788880
3.4 加入正则项,例如 L + 1 2 λ w 2 L+\frac{1}{2} \lambda w^2 L+21λw2
BP算法推导
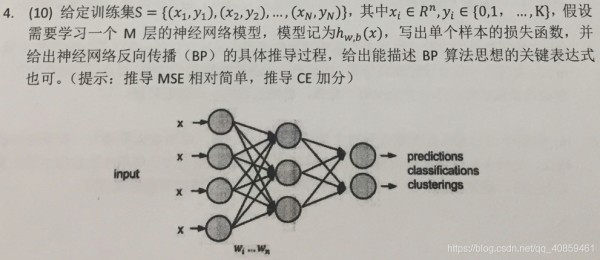
知乎: https://zhuanlan.zhihu.com/p/23270674
k-means 算法

K-means 算法流程:
K-means 聚类算法的弊端:
弊端1:初始聚类中心的位置和数目是随机选择的,可能会导致算法的收敛过慢
改进:K-Means++:
a) 从输入的数据点集合中随机选择一个点作为第一个聚类中心μ1
b) 对于数据集中的每一个点xi,计算它与已选择的聚类中心中最近聚类中心的距离
D ( x ) = m i n ∑ r = 1 k s e l e c t e d ∣ ∣ x i − u r ∣ ∣ 2 D(x)=min \sum_{r=1}^{k_{selected}} ||x_i-u_r||^2 D(x)=minr=1∑kselected∣∣xi−ur∣∣2
c) 选择一个新的数据点作为新的聚类中心,选择的原则是: D ( x ) D(x) D(x)较大的点,被选取作为聚类中心的概率较大
d) 重复b和c直到选择出k个聚类质心
e) 利用这k个质心来作为初始化质心去运行标准的K-Means算法
弊端2:每次迭代时需要计算全部样本点到聚类中心之间的距离,耗费时间较长
改进:距离计算优化 elkan K-Means
利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质,来减少距离的计算;
第一种规律是对于一个样本点 x x x和两个质心 μ j 1 , μ j 2 μ_{j_1},μ_{j_2} μj1,μj2。如果我们预先计算出了这两个质心之间的距离 D ( j 1 , j 2 ) D(j_1,j_2) D(j1,j2),则如果计算发现 2 D ( x , j 1 ) ≤ D ( j 1 , j 2 ) 2D(x,j_1)≤D(j_1,j_2) 2D(x,j1)≤D(j1,j2), 我们立即就可以知道 D ( x , j 1 ) ≤ D ( x , j 2 ) D(x, j_1)≤D(x, j_2) D(x,j1)≤D(x,j2)。此时我们不需要再计算 D ( x , j 2 ) D(x,j_2) D(x,j2), 也就是说省了一步距离计算;
第二种规律是对于一个样本点 x x x和两个质心 μ j 1 , μ j 2 μ_{j_1}, μ_{j_2} μj1,μj2。我们可以得到 D ( x , j 2 ) ≥ m a x 0 , D ( x , j 1 ) − D ( j 1 , j 2 ) D(x,j_2)≥max{0,D(x,j_1)−D(j_1,j_2)} D(x,j2)≥max0,D(x,j1)−D(j1,j2)。这个从三角形的性质也很容易得到;
大样本优化 Mini Batch K-Means
用样本集中的一部分的样本来做传统的K-Means,可以避免样本量太大时的计算难题,算法收敛速度大大加快,代价就是聚类的精确度也会有一些降低
编程题
NMS 
伪代码
假设有有一个候选的 boxes 的集合 B 和其对应的 scores 集合 S:
STEP1: 在集合 S 中找出置信度最高的样本 M;
STEP2: 将 M 对应的 box 从 B 中删除;
STEP3: 将删除的 box 添加到集合 D 中;
STEP4: 从 B 中删除与 M 对应的 box 重叠区域大于阈值的框;
STEP5: 判断 B 中是否为空,为空则结束,否则跳到STEP1;
python实现
import numpy as np def NMS(dets, thresh): """Pure Python NMS baseline.""" #x1、y1、x2、y2、以及score赋值 x1 = dets[:, 0] y1 = dets[:, 1] x2 = dets[:, 2] y2 = dets[:, 3] scores = dets[:, 4] #每一个候选框的面积 areas = (x2 - x1 + 1) * (y2 - y1 + 1) #order是按照score降序排序的 order = scores.argsort()[::-1] keep = [] while order.size > 0: i = order[0] keep.append(i) #计算当前概率最大矩形框与其他矩形框的相交框的坐标,得到的是向量 xx1 = np.maximum(x1[i], x1[order[1:]]) yy1 = np.maximum(y1[i], y1[order[1:]]) xx2 = np.minimum(x2[i], x2[order[1:]]) yy2 = np.minimum(y2[i], y2[order[1:]]) #计算相交框的面积,注意矩形框不相交时w或h算出来会是负数,用0代替 w = np.maximum(0.0, xx2 - xx1 + 1) h = np.maximum(0.0, yy2 - yy1 + 1) inter = w * h #计算重叠度IOU:重叠面积/(面积1+面积2-重叠面积) ovr = inter / (areas[i] + areas[order[1:]] - inter) #找到重叠度不高于阈值的矩形框索引 inds = np.where(ovr <= thresh)[0] #将order序列更新,由于前面得到的矩形框索引要比矩形框在原order序列中的索引小1,所以要把这个1加回来 order = order[inds + 1] return keep if __name__ == "__main__": dets = np.array([[30, 20, 230, 200, 1], [50, 50, 260, 220, 0.9], [210, 30, 420, 5, 0.8], [430, 280, 460, 360, 0.7]]) thresh = 0.35 keep_dets = NMS(dets, thresh) print(keep_dets) print(dets[keep_dets])
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748中位数
http://www.voidcn.com/article/p-peoomiwy-ra.html
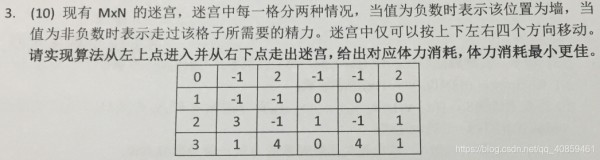
走迷宫
图像插值

知乎 https://zhuanlan.zhihu.com/p/45863015
发红包

最小金额0.01元;
所有人的总钱数为红包总金额;
最大金额为 红包总额-人数*0.01;
import random import numpy as np def redpackage(money, people): sum_m = 0 num = 0 result = [] while True: try: m = random.randint(1, money*100-people*1-sum_m) result.append(m/100.) sum_m += m num += 1 if num == people-1: break except: sum_m = 0 num = 0 result = [] continue result.append((money*100.-sum_m)/100.) return result if __name__ == '__main__': num = 100 while num > 0: res = redpackage(100, 10) print res, len(res), sum(res) num -= 1
123456789101112131415161718192021222324252627282930多线程


