粒子群算法求解无约束优化问题源码实现

发布时间：2025-05-05 19:59

量子计算机将实现超快计算，解决传统电脑无法处理的问题。 #生活知识# #科技生活# #科技改变生活# #未来科技产品#

算法原理

粒子群算法思想来源于实际生活中鸟捕食的过程。假设在一个n维的空间中，有一群鸟（m只）在捕食，食物位于n维空间的某个点上，对于第i只鸟某一时刻来说，有两个向量描述，一个是鸟的位置向量，第二个是鸟的速度。假设鸟能够判断一个位置的好坏，所谓“好坏”，就是离食物更近了还是更远了。鸟在捕食的过程中会根据自己的经验以及鸟群中的其他鸟的位置决定自己的速度，根据当前的位置和速度，可以得到下一刻的位置，这样每只鸟通过向自己和鸟群学习不断的更新自己的速度位置，最终找到食物，或者离食物足够近的点。更新速度和位置的表达式如下。

算法流程

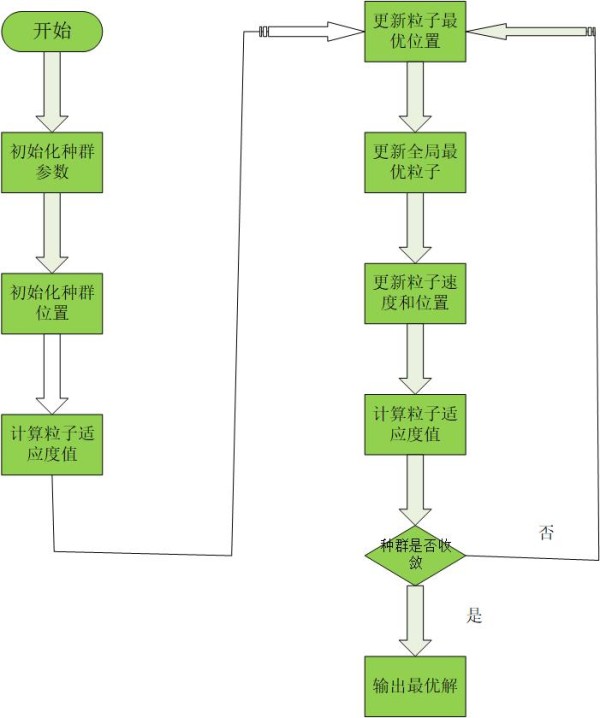
算例

语言python 3.7

求解下列函数的最小值

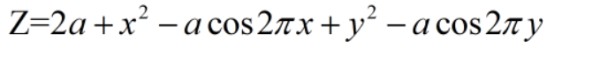
步骤1：绘制函数图像

设置a=10

import numpy as np import matplotlib.pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D # 生成X和Y的数据 X = np.arange(-5, 5, 0.1) Y = np.arange(-5, 5, 0.1) X, Y = np.meshgrid(X, Y) # 目标函数 A = 10 Z = 2 * A + X ** 2 - A * np.cos(2 * np.pi * X) + Y ** 2 - A * np.cos(2 * np.pi * Y) # 绘图 fig = plt.figure() ax = Axes3D(fig) surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm) plt.show() 1234567891011121314151617181920

可以发现此函数有很多尖波，有很多极大值和极小值。寻找全局最小值比较困难。

算法实现

由于有2个变量（x,y）假设有N个粒子，则V和X都是N*2的矩阵

# 速度 # Vi+1 = w*Vi + c1 * r1 * (pbest_i - Xi) + c2 * r2 * (gbest_i - Xi) # 位置 # Xi+1 = Xi + Vi+1 # vi, xi 分别表示粒子第i维的速度和位置 # pbest_i, gbest_i 分别表示某个粒子最好位置第i维的值、整个种群最好位置第i维的值 1234567

首先定义3个函数，分别是适应度函数fitness_func，速度更新函数velocity_update、位置更新函数position_update

import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体 mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题 def fitness_func(X): """计算粒子的的适应度值，也就是目标函数值，X 的维度是 size * 2 """ A = 10 pi = np.pi x = X[:, 0] y = X[:, 1] return 2 * A + x ** 2 - A * np.cos(2 * pi * x) + y ** 2 - A * np.cos(2 * pi * y) def velocity_update(V, X, pbest, gbest, c1, c2, w, max_val): """ 根据速度更新公式更新每个粒子的速度 #种群大小20 :param V: 粒子当前的速度矩阵，20*2 的矩阵 :param X: 粒子当前的位置矩阵，20*2 的矩阵 :param pbest: 每个粒子历史最优位置，20*2 的矩阵 :param gbest: 种群历史最优位置，1*2 的矩阵 """ size = X.shape[0]#种群大小 r1 = np.random.random((size, 1))#生成size 个 0-1之间的随机数 r2 = np.random.random((size, 1))#生成size 个 0-1之间的随机数 V = w * V + c1 * r1 * (pbest - X) + c2 * r2 * (gbest - X) # 直接对照公式写就好了 # 防止越界处理 V[V < -max_val] = -max_val V[V > max_val] = max_val return V def position_update(X, V): """ 根据公式更新粒子的位置 :param X: 粒子当前的位置矩阵，维度是 20*2 :param V: 粒子当前的速度举着，维度是 20*2 """ return X + V 123456789101112131415161718192021222324252627282930313233343536373839404142

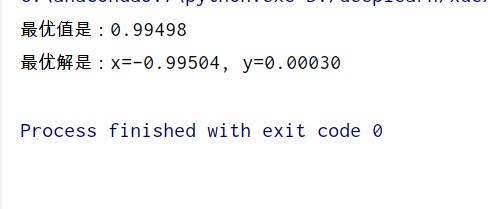
这是PSO 主函数，首先定义粒子群算法的参数，然后在每一轮的迭代中，更新局部最优和全局最优，直到满足最大迭代次数。

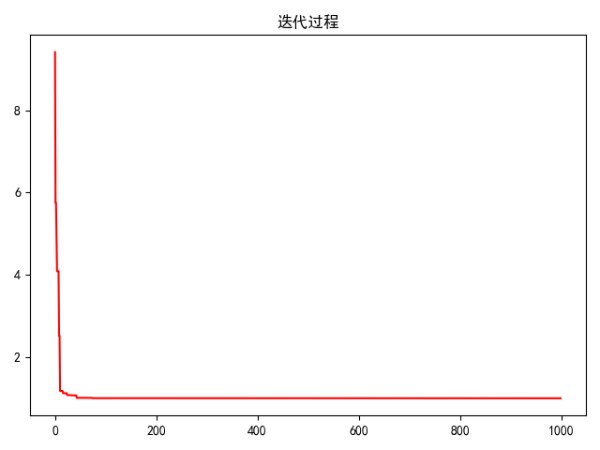
def pso(): # PSO的参数 w = 1 # 惯性因子，一般取1 c1 = 2 # 学习因子，一般取2 c2 = 2 # r1 = None # 为两个（0,1）之间的随机数 r2 = None dim = 2 # 维度的维度 size = 20 # 种群大小，即种群中小鸟的个数 iter_num = 1000 # 算法最大迭代次数 max_val = 0.5 # 限制粒子的最大速度为0.5 best_fitness = float(9e10) # 初始的适应度值，在迭代过程中不断减小这个值 fitneess_value_list = [] # 记录每次迭代过程中的种群适应度值变化 # 初始化种群的各个粒子的位置 # 用一个 20*2 的矩阵表示种群，每行表示一个粒子 X = np.random.uniform(-5, 5, size=(size, dim))#2维表示x、y # 初始化种群的各个粒子的速度 V = np.random.uniform(-0.5, 0.5, size=(size, dim))##2维表示x、y的速度 # 计算种群各个粒子的初始适应度值 p_fitness = fitness_func(X) # 计算种群的初始最优适应度值 g_fitness = p_fitness.min() # 讲添加到记录中 fitneess_value_list.append(g_fitness) # 初始的个体最优位置和种群最优位置 pbest = X gbest = X[p_fitness.argmin()] # 接下来就是不断迭代了 for i in range(1, iter_num): V = velocity_update(V, X, pbest, gbest, c1, c2, w, max_val) # 更新速度 X = position_update(X, V) # 更新位置 p_fitness2 = fitness_func(X) # 计算各个粒子的适应度 g_fitness2 = p_fitness2.min() # 计算群体的最优适应度 # 更新每个粒子的历史最优位置 for j in range(size): if p_fitness[j] > p_fitness2[j]: pbest[j] = X[j] p_fitness[j] = p_fitness2[j] # 更新群体的最优位置 if g_fitness > g_fitness2: gbest = X[p_fitness2.argmin()] g_fitness = g_fitness2 # 记录最优迭代结果 fitneess_value_list.append(g_fitness) # 迭代次数+1 i += 1 # 打印迭代的结果 print("最优值是：%.5f" % fitneess_value_list[-1]) print("最优解是：x=%.5f, y=%.5f" % (gbest[0],gbest[1])) # 最优值是：0.00000 # 最优解是：x=0.00000, y=-0.00000 # 绘图 plt.plot(fitneess_value_list, color='r') plt.title('迭代过程') plt.show() pso() 1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859