2022年数维杯数学建模C题电动汽车充电站的部署优化策略求解全过程文档及程序

发布时间：2025-05-08 09:37

定期对电动汽车进行智能充电模式设置，可以优化充电过程，节省能源。 #生活常识# #生活建议# #节能技巧# #电动汽车充电攻略#

2022年数维杯数学建模

C题电动汽车充电站的部署优化策略

原题再现：

近年来，随着化石能源的逐渐枯竭和环境污染的不断加剧，电动汽车（EV）作为传统燃油车的主要替代品之一，得到了快速的发展。据国际能源署统计，2019年全球电动私家车已达 7.2 百万辆，较 2018 年增长了 40% 。EV 公共充电设施为 EV 提供充电续航服务，也得到了快速发展。然而由于没有合理的统筹，公共充电设施存在利用率低、寻桩困难、充电等待时间长等问题，造成了土地、财政补贴、电力等资源的极大错配与浪费，大大降低了社会综合效益。本赛题旨在通过数学建模，为城市内公共充电站的选址和定容提供优化部署方案，提高社会综合效益。
由于充电站的建设与运营涉及多个利益主体，主要包括充电站建设运营商（简称充电站），EV 用户和电网等。各个利益主体的利益并不一致，例如，如果充电站加大投入，EV 用户将获得更高质量的充电服务，但充电站可能由于过高的充电设施闲置率和运维成本造成收益下降；反之，EV 用户将得不到可靠的充电服务，例如充电设施数量不足或距离过远，排队等待时间过长等。而电网方面主要考虑的是能源的整体利用效率和配电网络安全等。
EV 充电站部署的主要依据是 EV 用户充电需求的时空分布，充电需求的时空分布受到 EV 规模、出行行为和充电行为等因素的影响。一般来说，车流量大的地方充电需求旺盛，反之则充电需求较少。同时，城市功能区也会影响 EV 用户的充电行为，例如，EV 用户更倾向于选择饭店、超市、停车场等需要滞留的场所进行充电。由于大数据技术的兴起，数据驱动作为研究实际问题的方法之一被广泛采用 [3,4]。本赛题主要提供两个相关数据集，介绍如下：
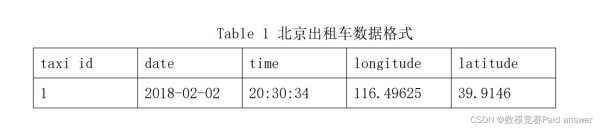
数据一：北京出租车轨迹数据（txt 格式），其包含了 10357 条北京出租车GPS 轨迹数据，时间段为 2018 年 2 月 2 号至 2 月 8 号。数据具体格式见 Table 1，具体数据见附件一，详细说明见附件三。
在这里插入图片描述
数据二：北京路网数据，该数据是从 OpenStreetMap 网站下载北京路网数据并由Python 模块 osm2gmns 提取得到。包含三个数据表（csv 格式），node，link 和
poi，分别记录了道路交叉口信息，道路信息和兴趣点信息。具体数据见附件二。
OpenStreetMap 网站：https://www.openstreetmap.org/
三个数据表说明详见：
https://osm2gmns.readthedocs.io/en/latest/gmns.html
通过数据一和数据二，可以构造出北京的真实路网和出租车的出行信息。参赛者可以自行选取所需数据，赛题之外的数据也被推荐使用，但需要注明出处。（需要注意的是，赛题提供的数据均处于 WGS 84 坐标系下）。
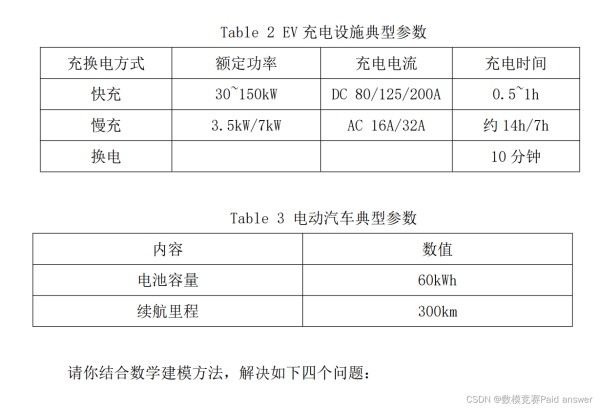
为了研究方便，赛题给出 EV 充电设施和 EV 的典型参数（仅供参考,参赛者可根据建模需要自行调整），分别如 Table 2, Table 3 所示
在这里插入图片描述
问题一：请你结合数据一和数据二，确定在当前的出租车数量规模下（假设所有出租车均是电动汽车）的最优充电桩位置及其数量分布结果。
问题二：请根据赛题所提供的数据及你能够搜集整理到的相关数据，预测北京市 2021 至 2025 年的 EV 用户充电需求的时空分布。（预测结果可以通过图或表格的形式进行展示）
问题三：基于问题二得到的充电需求时空分布，在问题一的基础上进一步提出充电桩的逐步扩充或减少的量化模型，并给出规划区域和时段内 EV 公共充电站的运营时间表。（最好将相关结果以可视化方式展示出来）。
问题四：在极端寒冷天气下，电动汽车的电量消耗会快速上升，这会使得充电桩的短时间充电需求过高，您能否根据问题二中的预测数据提供极端寒冷天气下的同时考虑充电和换电的最优方案？（换电是指直接更换同类型电池）
附件：
附件一：北京路网数据集
附件二：充电桩数据
附件三：充电桩数据集说明

整体求解过程概述(摘要)

新能源汽车是全球汽车产业绿色发展和转型升级的重要方向，也是我国汽车产业发展的一种战略选择．大力推进充电基础设施建设，有利于解决电动汽车充电难题，是新能源汽车产业发展的重要保障．本文解决了以下问题：
对于问题一：根据所给数据集确定最优的充电桩位置及数量分布，本文首先收集了北京 2018 年 2 月 2 日-8 日电动车共 10357 辆出租车的 GP S 轨迹数据，其次考虑定义为需求点的条件，最终确定间隔时间大于等于 30h 且速度小于 1KM/h，确定共有 95362 个需求点，进而建立基于距离的 K−Means 聚类模型，共将其聚为 17 类，需求点最多的 3 个类别其聚类中心坐标为（116.4821，39.95636）、（116.4235,39.86061）、（116.3103,39.89656），需求点个数分别为 16739,15428,13053．进而对 17 个类别继续聚类，最终得到最优的充电桩数量总计为 31397 个，详细结果如图 5-8．
对于问题二：需要预测北京市 2021-2025 年的 EV 用户充电需求的时空分布，本文首先在中国充电联盟爬取了数据，通过分析 pearson 相关系数可知，与北京公共充电桩数量相关程度最大的为新能源汽车保有量，其相关系数为 0.9923，因此通过预测新能源汽车保有量来预测用户需求的时空分布，新能源汽车保有量随时间的拟合回归方程为y1 = 102.82x−207215 ，拟合优度 R2 为 0.9891，北京公共充电桩数量 y2 = 134.8y1+3562.9，拟合优度 R2 为 0.9653，通过 2018 年需求量与北京公共充电桩数量比值 3.0373, 进而预测出需求分布的时空分布，类别最多的 3 类结果如表 5-8所示.
对于问题三：本文通过区域充电桩数量与总充电桩数量之比与问题二得到的用户需求时空分布数据确认充电桩数量，如 2023 年的充电桩需求量 36184，得出充电桩总数量108552，通过区域七对应的比值 0.01 得出 2023 年区域 7 的充电桩数量为 1085，较 2022年区域七数量 950 增加了 14.2%，通过该数值可逐步对充电桩进行扩充．并对充电数据，我们划分为高校、工作区和研究区三个充电区域，统计所有区域不同时间段充电数量得出 5 点到 13 点是充电高峰期，峰值出现在 7 点左右，在这个时段我们可开放更多充电桩；统计所有区域周末和工作日充电数量得出工作日充电量占总数 91%，周末只有 9%，我们可在周末减少充电桩运营时间以降低运营成本．
对于问题四：本文通过站点各月的总充电时长和总充电量统计，得出 10 月至 2 月较其他月份真实充电量增加约 31.48%，故应更改充电站充换点方案以满足用户需求．

问题分析：

题目数据集包含来自加州理工大学的三个充电站充电桩数据、北京路网数据，其中包含：道路交叉口信息、道路信息、景点信息．根据北京出租车轨迹数据以及北京路网数据，以这部分数据得到用户轨迹信息并得到用户的时空分布，分析其充电需求给出最优的充电桩位置及数量．由于极端寒冷天气、大型国际活动、节假日出行等多个方面都可能对充电桩需求带来影响，考虑这些因素的影响并给出最优方案．
对问题 1 研究的意义的分析．问题 1 需要根据题目所提到的北京出租车轨迹数据对充电桩位置及数量进行规划，对于解决此问题，我们首先分析建立一个充电站的需求是从何而来，题目所提到出租车司机用户存在充电需求一般分为三个方面：1. 车辆电量达到阈值；2. 换班或下班；3. 三餐期间；我们将一个用户可能存在充电需求的经纬度坐标定义为一个需求点．其次需要考虑到尽可能多的需求点．根据北京出租车轨迹数据停留时间长短及坐标变化确定需求点，将需求点数据进行多次聚类，首先得到大区域，再将各区域划分为小区域并得到充电桩数量．
对问题 2 研究的意义的分析．问题 2 要求根据题目所给数据或收集的
数据对北京未来几年用户充电需求的时空分布进行预测，我们需要获得此前用户充电需求的趋势变化，根据趋势变化对未来进行预测．由于题目所给数据量较小，故需要对各年北京市 EV 用户数量数据进行收集，并考虑国际能源价格趋势、国内政策扶持、用户对新能源车型的评价等多个方面对
充电需求的影响，最终根据问题一所得时空分布，得到结果：北京市 2021至 2025 年的 EV 用户充电需求的时空分布．
对问题 3 研究的意义的分析．问题 2 中我们已得未来北京市充电需求时空分布，由于未来新能源车的发展，其充电需求与第一问数据相较有所变化，而我们所规划的充电桩位置及数量应在未来几年甚至几十年都能有效利用，故需要根据问题 2 所得“北京未来几年用户充电需求的时空分布”情况将问题 1 规划结果进行修正，并根据各区域用户习惯、出行规律等条件，规划出区域充电站的运营时间表．
对问题 4 研究的意义的分析．在前面三个问题中，均根据用户自身的
需求对充电桩位置及数量进行规划，在问题 4 中，加入了外来因素的影响，例如题目所说极端寒冷天气对汽车电量的影响，以及由于大型事件、节假日造成外来车辆激增，这些都会使充电桩的短时间充电需求过高，若根据短时间的需求增加充电桩的数量，则会增加充电站运营成本．故我们需要根据外来因素影响所造成的需求量变化再次规划充电桩的位置及数量、充电桩的类型、以及换电站的设置．在附件一中，我们可以得到三个充电站接近三年的充电数据，根据这部分数据可以分析用户充电习惯、车辆充电类型分布等多方面数据．

模型假设：

1. 假设数据集中出租车均为同质纯电动车；
2. 假设题目所给电动汽车典型参数为出租车实际参数；
3. 出租车司机会选择可接受范围内较近的充电站进行充电；
4. 任何充电站的任何一个充电桩都只能为一辆电动汽车服务；

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可非慈善耶稣论文缩略图：

在这里插入图片描述

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可非慈善耶稣程序代码：

import warnings import pandas as pd import numpy as np import seaborn as sns import matplotlib . pyplot as plt import datetime import matplotlib . font_manager as fm from statsmodels . graphics . api import qqplot from datetime import datetime plt . rcParams ['font .sans - serif '] = ['SimHei '] # 中文字体设置 - 黑体 plt . rcParams ['axes . unicode_minus '] = False # 解决保存图像是负号 '-' 显示为方块的问题 # 解决 Seaborn 中文显示问题 sns . set ( font ='SimHei ', font_scale =1) # 解决 Seaborn 中文显示问题 fig = plt . figure () warnings . filterwarnings (" ignore ") # 读取数据表 df1 = pd . read_excel (r'juleidata . xlsx ') julei_data = df1 . iloc [: ,2:4] np . array ( julei_data ) import numpy as np import matplotlib . pyplot as plt # 两点距离 def distance ( e1 , e2 ): return np . sqrt (( e1 [0] - e2 [0])**2+( e1 [1] - e2 [1])**2) # 集合中心 def means ( arr ): return np . array ([ np . mean ([ e [0] for e in arr ]) , np . mean ([ e [1] for e in arr ])]) # arr 中距离 a 最远的元素，用于初始化聚类中心 def farthest ( k_arr , arr ): f = [0 , 0] max_d = 0 for e in arr : d = 0 for i in range ( k_arr . __len__ ()): d = d + np . sqrt ( distance ( k_arr [ i ] , e )) if d > max_d : max_d = d f = e return f # arr 中距离 a 最近的元素，用于聚类 def closest (a , arr ): c = arr [1] min_d = distance (a , arr [1]) arr = arr [1:] for e in arr : d = distance (a , e ) if d < min_d : min_d = d c = e return c if __name__ ==" __main__ ": ## 生成二维随机坐标，手上有数据集的朋友注意，理解 arr 改起来就很容易了 ## arr 是一个数组，每个元素都是一个二元组，代表着一个坐标 ## arr 形如：[ (x1 , y1), (x2 , y2) , (x3 , y3) ... ] arr = np . array ( julei_data ) ## 初始化聚类中心和聚类容器 m = 17#l 类别数 r = np . random . randint ( arr . __len__ () - 1) k_arr = np . array ([ arr [ r ]]) cla_arr = [[]] for i in range (m -1): k = farthest ( k_arr , arr ) k_arr = np . concatenate ([ k_arr , np . array ([ k ])]) cla_arr . append ([]) ## 迭代聚类 n = 20 cla_temp = cla_arr for i in range ( n ): # 迭代 n次 for e in arr : # 把集合里每一个元素聚到最近的类 ki = 0 # 假定距离第一个中心最近 min_d = distance (e , k_arr [ ki ]) for j in range (1 , k_arr . __len__ ()): if distance (e , k_arr [ j ]) < min_d : # 找到更近的聚类中心 min_d = distance (e , k_arr [ j ]) ki = j cla_temp [ ki ]. append ( e ) # 迭代更新聚类中心 for k in range ( k_arr . __len__ ()): if n - 1 == i : break k_arr [ k ] = means ( cla_temp [ k ]) cla_temp [ k ] = [] ## 可视化展示 col = ['HotPink ', 'Chartreuse ', ' LightSalmon ', 'pink ', '#359 aff ', 'red ','Aqua ', 'Chartreuse ', 'yellow ', '#6 b9bc2 ', '#9687 ed ','HotPink ', 'Chartreuse ', ' LightSalmon ', 'pink ', '#359 aff ', 'red '] for i in range ( m ): plt . scatter ( k_arr [ i ][0] , k_arr [ i ][1] , linewidth =10 , color = col [ i ])# 聚类中心点 plt . scatter ([ e [0] for e in cla_temp [ i ]] , [ e [1] for e in cla_temp [ i ]] , color = col [ i ]) plt . show () from sklearn . cluster import KMeans kmeans = KMeans ( n_clusters =17 , random_state =123). fit ( julei_data ) # 简答打印结果 r1 = pd . Series ( kmeans . labels_ ). value_counts () r2 = pd . DataFrame ( kmeans . cluster_centers_ ) r = pd . concat ([ r2 , r1 ] , axis =1) r . columns = list ( julei_data . columns )+[ u' 类别数目 '] print (r ) # 详细输出原结果 r_new = pd . concat ([ pd . DataFrame ( julei_data ) , pd . Series ( kmeans . labels_ )] , axis =1) r_new . columns = list ( julei_data . columns )+[ u' 类别数目 '] # 导包 # coding : utf8 import pandas as pd import numpy as np import matplotlib import matplotlib . pyplot as plt import sys from matplotlib . ticker import MaxNLocator from collections import namedtuple from matplotlib . font_manager import FontProperties import seaborn as sns from matplotlib . pyplot import MultipleLocator from datetime import datetime font_set = FontProperties ( fname = r" *** path ***/ mpl - data / fonts / simfang . ttf ") matplotlib . rcParams ['figure . figsize '] matplotlib . rcParams ['savefig .dpi '] plt . rcParams ['font .sans - serif '] = ['SimHei '] # 解决中文显示问题 plt . rcParams ['axes . unicode_minus '] = False # 解决中文显示问题 plt . figure ( figsize =(15 , 10)) plt . rcParams ['font . size '] = 20 from math import radians , cos , sin , asin , sqrt # 问题一文件读取 data = pd . read_csv (r'taxi . csv ') # 画经纬度分布图 sns . set ( style ='darkgrid ') plt . figure ( figsize =(10 ,10)) sns . relplot ( x ='longitude ', y ='latitude ', data = data ) plt . show () # 删除北京之外的经纬度 data = data . loc [ data ['longitude '] >=115.416827 ,:] data = data . loc [ data ['longitude '] <=117.508251 ,:] data = data . loc [ data ['latitude '] >=39.442078 ,:] data = data . loc [ data ['latitude '] <=41.058964 ,:] # 画经纬度分布图 sns . set ( style ='darkgrid ') sns . relplot ( x ='longitude ', y ='latitude ', data = data ) plt . show () # 字符串转时间 data ['date time '] = data ['date time ']. apply ( lambda x : datetime . strptime (x ,'%Y -%m -%d %H:%M:%S')) # 重置索引 data = data . reset_index ( drop = True ) # 经纬度计算函数 def haversine ( lon1 , lat1 , lon2 , lat2 ): # 经度 1，纬度 1，经度 2，纬度 2 （十进制度数） """ Calculate the great circle distance between two points on the earth ( specified in decimal degrees ) """ # 将十进制度数转化为弧度 lon1 , lat1 , lon2 , lat2 = map ( radians , [ lon1 , lat1 , lon2 , lat2 ]) # haversine 公式 dlon = lon2 - lon1 dlat = lat2 - lat1 a = sin ( dlat /2)**2 + cos ( lat1 ) * cos ( lat2 ) * sin ( dlon /2)**2 c = 2 * asin ( sqrt ( a )) r = 6371 # 地球平均半径，单位为公里 return c * r * 1000 # 选出间隔时间大于等于 30 的数据 time = pd . DataFrame ( columns =[ 'taxi id ','date time ','longitude ','latitude ']) for i in range (1 , len ( data )): if( data ['taxi id '][ i ]== data ['taxi id '][ i -1]): # dis = haversine ( data [ ' longitude '][i], data [ ' latitude '][i], data [ ' longitude '][i -1] , data [ ' latitude '][i -1]) tim =( data ['date time '][ i ] - data ['date time '][ i -1]). total_seconds ()/60 if( tim >=30): time = time . append ( pd . DataFrame ([ data . loc [i -1 ,:]. values ] , columns =[ 'taxi id ','date time ','longitude ','latitude '])) # 计算汽车不同点坐标速度 time = time . reset_index ( drop = True ) sudu =[] for i in range (1 , len ( time )): if( time ['taxi id '][ i ]== time ['taxi id '][ i -1]): dis = haversine ( time ['longitude '][ i ] , time ['latitude '][ i ] , time ['longitude '][ i -1] , time ['latitude '][ i -1]) tim =( time ['date time '][ i ] - time ['date time '][ i -1]). total_seconds ()/60 if( tim !=0): su =( dis /( tim *60)) sudu . append ( su ) # 筛选出符合条件的需求点 sudu = pd . DataFrame () for i in range (1 , len ( time )): if( time ['taxi id '][ i ]== time ['taxi id '][ i -1]): dis = haversine ( time ['longitude '][ i ] , time ['latitude '][ i ] , time ['longitude '][ i -1] , time ['latitude '][ i -1]) tim =( time ['date time '][ i ] - time ['date time '][ i -1]). total_seconds ()/60 if( tim !=0): su =( dis /( tim *60)) # tim =( data [ ' date time '][i] - data [' date time '][i -1]). total_seconds ()/60 if( su >=0 and su <=1): sudu = sudu . append ( pd . DataFrame ([ time . loc [i -1 ,:]. values ] , columns =[ 'taxi id ','date time ','longitude ','latitude ']))

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185 全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可非慈善耶稣

网址：2022年数维杯数学建模C题电动汽车充电站的部署优化策略求解全过程文档及程序 https://www.yuejiaxmz.com/news/view/941290

⬅️上一篇：人民日报微观：电动车充电的精细治

➡️下一篇：新技术十分钟完成电动汽车充电