利用斐波那契数列测试递归及非递归算法的时间复杂度（工具：VS2015、C++，赠送精确计算耗时的类代码）

使用递归神经网络处理序列数据，如自然语言理解和时间序列预测 #生活技巧# #学习技巧# #深度学习技巧#

业余时间看了些关于时间复杂度的资料，就想着根据资料写个代码测试一下，本人尚属菜鸟，欢迎各位看官提出宝贵意见及建议~

斐波那契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=Fn-1+Fn-2（n>=2，n∈N*），用文字来说，就是斐波那契数列由 0 和 1 开始，之后的斐波那契数列系数就由之前的两数相加。

1.在VS2015中新建Win32控制台应用程序
2.代码如下：（各位可将如下代码直接复制到.cpp文件中运行）

// FibonacciSequence.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include "stdlib.h" #include "windows.h" class chronograph//计算时间用的结构体 { public:chronograph(){QueryPerformanceFrequency(&m_freq);QueryPerformanceCounter(&m_bgn);}void start(){QueryPerformanceCounter(&m_bgn);}double duration(){QueryPerformanceCounter(&m_end);return (m_end.QuadPart - m_bgn.QuadPart) * 1000.0 / m_freq.QuadPart;}LARGE_INTEGER now(){LARGE_INTEGER now;QueryPerformanceCounter(&now);return now;}double DoubleNow(){LARGE_INTEGER now;QueryPerformanceCounter(&now);return now.QuadPart*1000.0 / m_freq.QuadPart;} private:LARGE_INTEGER m_freq;LARGE_INTEGER m_bgn;LARGE_INTEGER m_end; }; int Fibonacci1(int n)//递归算法,时间复杂度O(2^n) {if (n<3){return 1;}else{return (Fibonacci1(n - 2) + Fibonacci1(n - 1));} } int Fibonacci2(int n)//非递归算法,时间复杂度O(n) {if (n<3){return 1;}else{int n1, n2, n3;n1 = 1;n2 = 1;n3 = n1 + n2;for (int j = 0; j < n - 2; j++){n3 = n1 + n2;n1 = n2;n2 = n3;}return n3;} } int main() {int nInt = 0;char * cIn = (char*)malloc(1024);chronograph chroTime;while (true){printf("请输入需要计算第几个斐波那契数列：\n");gets_s(cIn, 10);nInt = atoi(cIn);//非递归算法：chroTime.start();int nOut2 = Fibonacci2(nInt);double dtime2 = chroTime.duration();//递归算法：chroTime.start();int nOut1 = Fibonacci1(nInt);double dtime1 = chroTime.duration();printf("第%d个斐波那契数列值为：\n%d , 计算耗时：%f毫秒(递归算法)\n%d , 计算耗时：%f毫秒(非递归算法)\n\n", nInt, nOut1, dtime1, nOut2,dtime2);} return 0; }

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495

运行结果如下：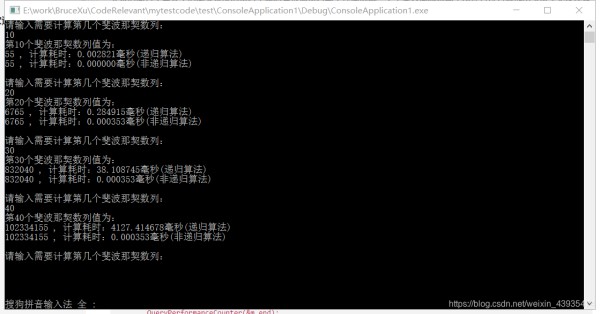

可以看到，如果使用递归算法计算斐波那契数列的话，会非常耗时，当计算到第40个数的时候，用时4s多，之后每多计算一个数字，耗时就会翻一倍！
结论：
递归算法,时间复杂度O(2^n)
非递归算法,时间复杂度O(n)

网址：利用斐波那契数列测试递归及非递归算法的时间复杂度（工具：VS2015、C++，赠送精确计算耗时的类代码） https://www.yuejiaxmz.com/news/view/989026

相关内容

递归算法入门：斐波那契、阶乘、倒序与排列实例解析
从“数学归纳法”到理解“递归算法”！
斐波拉契数列=>多种方法的比较（分治、递归、动态规划/递推）
数据结构之算法的时间与空间复杂度
【时间复杂度】时间复杂度优化法则简讲
递归算法详解
递归优化技巧
深入解析算法效率核心：时间与空间复杂度概览及优化策略
关于斐波那契数列 组合错排问题和一些递推公式合集整理
算法优化大揭秘：12个加速算法运行速度的实用技巧

随便看看