旅游省钱大法：加权最短路径

发布时间：2024-11-10 14:30

毕业季，对过去也许有些欢乐和感伤，对未来也许有些迷茫和向往，不过这些终究是过眼云烟，迟早会被时间淡化和遗忘。

在这段美好时光的末尾，确实应该来一场说走就走的毕业旅行，放肆一把，给青春画上一个完美的句号。

那么，本文就教给你一个动态规划算法，在毕业旅行中省钱，节约追求诗和远方的资本。

假设，你准备从学校所在的城市出发，游历多个城市，一路浪到公司入职，那么你应该如何安排旅游路线，才能最小化机票的开销？

我们来看看力扣第 787 题「K 站中转内最便宜的航班」：

787. K 站中转内最便宜的航班 | 力扣 | LeetCode |

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。如果不存在这样的路线，则输出 -1。

示例 1：

输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 1 输出: 200 解释: 城市航班图如下从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200，如图中红色所示。

示例 2：

输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 0 输出: 500 解释: 城市航班图如下从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500，如图中蓝色所示。

提示：

1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104航班没有重复，且不存在自环0 <= src, dst, k < nsrc != dst

函数签名如下：

java

int findCheapestPrice(int n, int[][] flights, int src, int dst, int K);

cpp

int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K);

python

def findCheapestPrice(n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:

func findCheapestPrice(n int, flights [][]int, src int, dst int, K int) int {}

javascript

var findCheapestPrice = function(n, flights, src, dst, K) {}

很明显，这题就是个加权有向图中求最短路径的问题。

说白了，就是给你一幅加权有向图，让你求 src 到 dst 权重最小的一条路径，同时要满足，这条路径最多不能超过 K + 1 条边（经过 K 个节点相当于经过 K + 1 条边）。

我们来分析下求最短路径相关的算法。

BFS 算法思路

我们前文 BFS 算法框架详解中说到，求最短路径，肯定可以用 BFS 算法来解决。

因为 BFS 算法相当于从起始点开始，一步一步向外扩散，那当然是离起点越近的节点越先被遍历到，如果 BFS 遍历的过程中遇到终点，那么走的肯定是最短路径。

不过呢，我们在 BFS 算法框架详解用的是普通的队列 Queue 来遍历多叉树，而对于加权图的最短路径来说，普通的队列不管用了，得用优先级队列 PriorityQueue。

为什么呢？也好理解，在多叉树（或者扩展到无权图）的遍历中，与其说边没有权重，不如说每条边的权重都是 1，起点与终点之间的路径权重就是它们之间「边」的条数。

这样，按照 BFS 算法一步步向四周扩散的逻辑，先遍历到的节点和起点之间的「边」更少，累计的权重当然少。

换言之，先进入 Queue 的节点就是离起点近的，路径权重小的节点。

但对于加权图，路径中边的条数和路径的权重并不是正相关的关系了，有的路径可能边的条数很少，但每条边的权重都很大，那显然这条路径权重也会很大，很难成为最短路径。

比如题目给的这个例子：

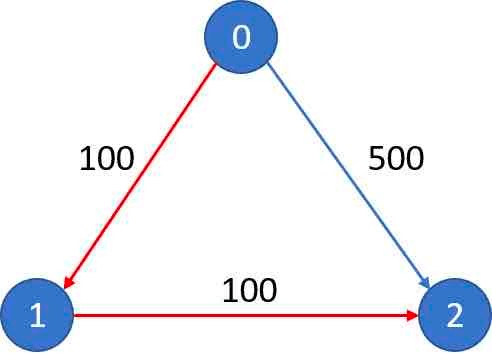
你是可以一步从 0 走到 2，但路径权重不见得是最小的。

所以，对于加权图的场景，我们需要优先级队列「自动排序」的特性，将路径权重较小的节点排在队列前面，以此为基础施展 BFS 算法，也就变成了 Dijkstra 算法。

说了这么多 BFS 算法思路，只是帮助大家融会贯通一下，我们本文准备主要讲解如何使用动态规划来解决这道题。关于 Dijkstra 算法的实现代码，文末有写，供读者参考。

动态规划思路

我们前文动态规划核心套路详解中说过，求最值的问题，很多都可能使用动态规划来求解。

加权最短路径问题，再加个 K 的限制也无妨，不也是个求最值的问题嘛，动态规划统统拿下。

我们先不管 K 的限制，单就「加权最短路径」这个问题来看看，它怎么就是个动态规划问题了呢？

比方说，现在我想计算 src 到 dst 的最短路径：

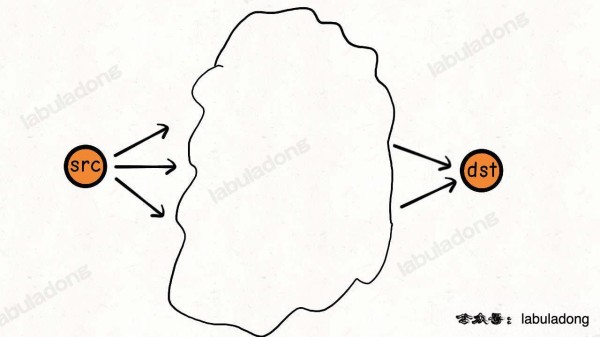
最小权重是多少？我不知道。

但我可以把问题进行分解：

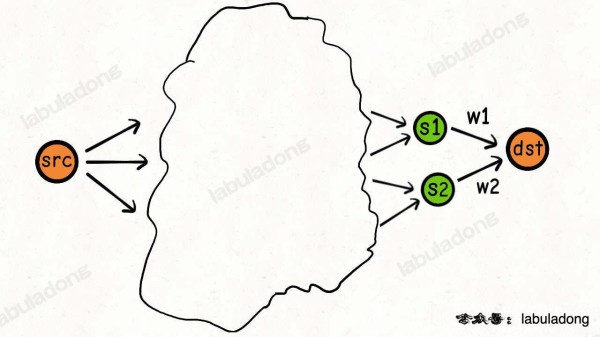
s1, s2 是指向 dst 的相邻节点，它们之间的权重我是知道的，分别是 w1, w2。

只要我知道了从 src 到 s1, s2 的最短路径，我不就知道 src 到 dst 的最短路径了吗！

minPath(src, dst) = min( minPath(src, s1) + w1, minPath(src, s2) + w2 )

这其实就是递归关系了，就是这么简单。

不过别忘了，题目对我们的最短路径还有个「路径上不能超过 K + 1 条边」的限制。

那么我们不妨定义这样一个 dp 函数：

python

def dp(s: int, k: int) -> int:

func dp(s int, k int) int {}

javascript

var dp = function(s, k) {}

函数的定义如下：

从起点 src 出发，k 步之内（一步就是一条边）到达节点 s 的最小路径权重为 dp(s, k)。

那么，dp 函数的 base case 就显而易见了：

java

// 定义：从 src 出发，k 步之内到达 s 的最小成本 int dp(int s, int k) { // 从 src 到 src，一步都不用走 if (s == src) { return 0; } // 如果步数用尽，就无解了 if (k == 0) { return -1; } // ... }

cpp

python

# 定义：从 src 出发，k 步之内到达 s 的最小成本 def dp(s: int, k: int) -> int: # 从 src 到 src，一步都不用走 if s == src: return 0 # 如果步数用尽，就无解了 if k == 0: return -1 # ...

// 定义：从 src 出发，k 步之内到达 s 的最小成本 func dp(s, k int) int { // 从 src 到 src，一步都不用走 if s == src { return 0 } // 如果步数用尽，就无解了 if k == 0 { return -1 } // ... }

javascript

// 定义：从 src 出发，k 步之内到达 s 的最小成本 var dp = function(s, k) { // 从 src 到 src，一步都不用走 if (s === src) { return 0; } // 如果步数用尽，就无解了 if (k === 0) { return -1; } // ... }

题目想求的最小机票开销就可以用 dp(dst, K+1) 来表示：

java

int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) { // 将中转站个数转化成边的条数 K++; // ... return dp(dst, K); }

cpp

int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) { // 将中转站个数转化成边的条数 K++; // ... return dp(dst, K); }

python

def findCheapestPrice(n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int: # 将中转站个数转化成边的条数 K += 1 #... return dp(dst, K)

func findCheapestPrice(n int, flights [][]int, src int, dst int, K int) int { // 将中转站个数转化成边的条数 K++ // ... return dp(dst, K) }

javascript

var findCheapestPrice = function(n, flights, src, dst, K) { // 将中转站个数转化成边的条数 K++; // ... return dp(dst, K); };

添加了一个 K 条边的限制，状态转移方程怎么写呢？其实和刚才是一样的：

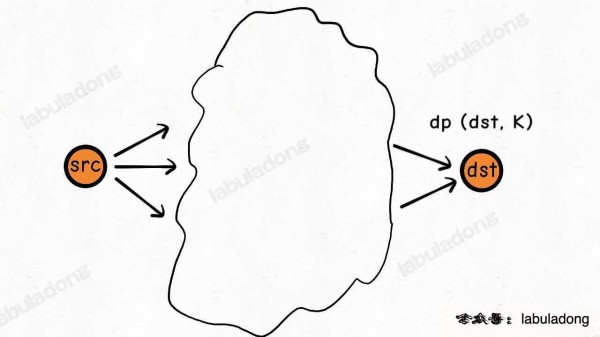
K 步之内从 src 到 dst 的最小路径权重是多少？我不知道。

但我可以把问题分解：

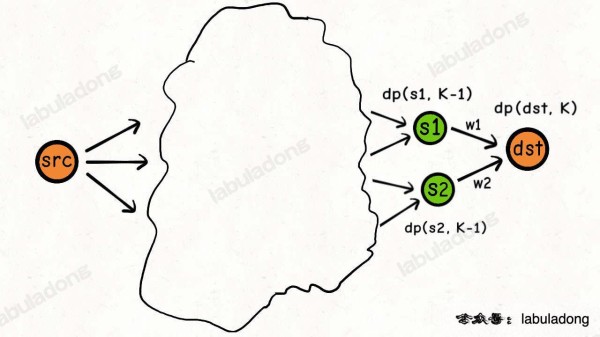
s1, s2 是指向 dst 的相邻节点，我只要知道 K - 1 步之内从 src 到达 s1, s2，那我就可以在 K 步之内从 src 到达 dst。

也就是如下关系式：

dp(dst, k) = min( dp(s1, k - 1) + w1, dp(s2, k - 1) + w2 )

这就是新的状态转移方程，如果你能看懂这个算式，就已经可以解决这道题了。

代码实现

根据上述思路，我怎么知道 s1, s2 是指向 dst 的相邻节点，他们之间的权重是 w1, w2？

我希望给一个节点，就能知道有谁指向这个节点，还知道它们之间的权重，对吧。

专业点说，得用一个数据结构记录每个节点的「入度」indegree，即存储所有指向该节点的相邻节点，以及它们之间边的权重。

具体看代码吧，我们用一个哈希表 indegree 存储入度，然后实现 dp 函数：

java

class Solution { // 哈希表记录每个点的入度，键是节点编号，值是指向该节点的相邻节点以及之间的权重 // to -> [from, price] HashMap<Integer, List<int[]>> indegree; int src, dst; public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) { // 将中转站个数转化成边的条数 K++; this.src = src; this.dst = dst; indegree = new HashMap<>(); for (int[] f : flights) { int from = f[0]; int to = f[1]; int price = f[2]; // 记录谁指向该节点，以及之间的权重 indegree.putIfAbsent(to, new LinkedList<>()); indegree.get(to).add(new int[] {from, price}); } return dp(dst, K); } // 定义：从 src 出发，k 步之内到达 s 的最短路径权重 int dp(int s, int k) { // base case if (s == src) { return 0; } if (k == 0) { return -1; } // 初始化为最大值，方便等会取最小值 int res = Integer.MAX_VALUE; if (indegree.containsKey(s)) { // 当 s 有入度节点时，分解为子问题 for (int[] v : indegree.get(s)) { int from = v[0]; int price = v[1]; // 从 src 到达相邻的入度节点所需的最短路径权重 int subProblem = dp(from, k - 1);

// 跳过无解的情况 if (subProblem != -1) { res = Math.min(res, subProblem + price); } } } // 如果还是初始值，说明此节点不可达 return res == Integer.MAX_VALUE ? -1 : res; } }

cpp

class Solution { public: // 哈希表记录每个点的入度，键是节点编号，值是指向该节点的相邻节点以及之间的权重 // to -> [from, price] unordered_map<int, vector<pair<int, int>>> indegree; int src, dst; int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) { // 将中转站个数转化成边的条数 K++; this->src = src; this->dst = dst; for(const auto& f : flights) { int from = f[0]; int to = f[1]; int price = f[2]; // 记录谁指向该节点，以及之间的权重 indegree[to].push_back(make_pair(from, price)); } return dp(dst, K); } // 定义：从 src 出发，k 步之内到达 s 的最短路径权重 int dp(int s, int k) { // base case if (s == src) { return 0; } if (k == 0) { return -1; } // 初始化为最大值，方便等会取最小值 int res = INT_MAX; if (indegree.count(s)) { // 当 s 有入度节点时，分解为子问题 for(const auto& v : indegree[s]) { int from = v.first; int price = v.second; // 从 src 到达相邻的入度节点所需的最短路径权重 int subProblem = dp(from, k - 1);

// 跳过无解的情况 if (subProblem != -1) { res = min(res, subProblem + price); } } } // 如果还是初始值，说明此节点不可达 return res == INT_MAX ? -1 : res; } };

python

class Solution: def __init__(self): # 哈希表记录每个点的入度，键是节点编号，值是指向该节点的相邻节点以及之间的权重 # to -> [from, price] self.indegree = {} self.src = 0 self.dst = 0 def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int: # 将中转站个数转化成边的条数 K += 1 self.src = src self.dst = dst for f in flights: from_, to, price = f # 记录谁指向该节点，以及之间的权重 if to not in self.indegree: self.indegree[to] = [] self.indegree[to].append([from_, price]) return self.dp(dst, K) # 定义：从 src 出发，k 步之内到达 s 的最短路径权重 def dp(self, s: int, k: int) -> int: # base case if s == self.src: return 0 if k == 0: return -1 # 初始化为最大值，方便等会取最小值 res = float('inf') if s in self.indegree: # 当 s 有入度节点时，分解为子问题 for v in self.indegree[s]: from_, price = v # 从 src 到达相邻的入度节点所需的最短路径权重 subProblem = self.dp(from_, k - 1)

# 跳过无解的情况 if subProblem != -1: res = min(res, subProblem + price) # 如果还是初始值，说明此节点不可达 return -1 if res == float('inf') else res

func findCheapestPrice(n int, flights [][]int, src, dst, K int) int { // 哈希表记录每个点的入度，键是节点编号，值是指向该节点的相邻节点以及之间的权重 // to -> [from, price] indegree := make(map[int][][2]int) // 将中转站个数转化成边的条数 K++ for _, f := range flights { from, to, price := f[0], f[1], f[2] // 记录谁指向该节点，以及之间的权重 indegree[to] = append(indegree[to], [2]int{from, price}) } return dp(src, dst, K, indegree) } // 定义：从 src 出发，k 步之内到达 s 的最小成本 func dp(src, s, k int, indegree map[int][][2]int) int { // base case if s == src { return 0 } if k == 0 { return -1 } // 初始化为最大值，方便等会取最小值 res := math.MaxInt32 if v, ok := indegree[s]; ok { // 当 s 有入度节点时，分解为子问题 for _, p := range v { from, price := p[0], p[1] // 从 src 到达相邻的入度节点所需的最短路径权重 subProblem := dp(src, from, k - 1, indegree)

// 跳过无解的情况 if subProblem != -1 { res = min(res, subProblem + price) } } } // 如果还是初始值，说明此节点不可达 if res == math.MaxInt32 { return -1 } return res }

javascript

// 跳过无解的情况 if (subProblem !== -1) { res = Math.min(res, subProblem + price); } } } // 如果还是初始值，说明此节点不可达 return res === Infinity ? -1 : res; };

有之前的铺垫，这段解法逻辑应该是很清晰的。当然，对于动态规划问题，肯定要消除重叠子问题。

为什么有重叠子问题？很简单，如果某个节点同时指向两个其他节点，那么这两个节点就有相同的一个入度节点，就会产生重复的递归计算。

怎么消除重叠子问题？找问题的「状态」。

状态是什么？在问题分解（状态转移）的过程中变化的，就是状态。

谁在变化？显然就是 dp 函数的参数 s 和 k，每次递归调用，目标点 s 和步数约束 k 在变化。

所以，本题的状态有两个，应该算是二维动态规划，我们可以用一个 memo 二维数组或者哈希表作为备忘录，减少重复计算。

我们选用二维数组做备忘录吧，注意 K 是从 1 开始算的，所以备忘录初始大小要再加一：

java

class Solution { int src, dst; HashMap<Integer, List<int[]>> indegree; // 备忘录 int[][] memo; public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) { K++; this.src = src; this.dst = dst; // 初始化备忘录，全部填一个特殊值 memo = new int[n][K + 1]; for (int[] row : memo) { Arrays.fill(row, -888); } indegree = new HashMap<>(); for (int[] f : flights) { int from = f[0]; int to = f[1]; int price = f[2]; indegree.putIfAbsent(to, new LinkedList<>()); indegree.get(to).add(new int[] {from, price}); } return dp(dst, K); } // 定义：从 src 出发，k 步之内到达 s 的最小成本 int dp(int s, int k) { // base case if (s == src) { return 0; } if (k == 0) { return -1; } // 查备忘录，防止冗余计算 if (memo[s][k] != -888) { return memo[s][k]; } // 状态转移代码不变 int res = Integer.MAX_VALUE; if (indegree.containsKey(s)) { for (int[] v : indegree.get(s)) { int from = v[0]; int price = v[1]; int subProblem = dp(from, k - 1);

if (subProblem != -1) { res = Math.min(res, subProblem + price); } } } // 存入备忘录 memo[s][k] = res == Integer.MAX_VALUE ? -1 : res; return memo[s][k]; } }

cpp

class Solution { int src, dst; unordered_map<int, vector<vector<int>>> indegree; // 备忘录 vector<vector<int>> memo; public: int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) { K++; this->src = src; this->dst = dst; // 初始化备忘录，全部填一个特殊值 memo = vector<vector<int>>(n, vector<int>(K + 1, -888)); for(const auto& f : flights) { int from = f[0]; int to = f[1]; int price = f[2]; indegree[to].push_back({from, price}); } return dp(dst, K); } // 定义：从 src 出发，k 步之内到达 s 的最小成本 int dp(int s, int k) { // base case if (s == src) { return 0; } if (k == 0) { return -1; } // 查备忘录，防止冗余计算 if (memo[s][k] != -888) { return memo[s][k]; } // 状态转移代码不变 int res = INT_MAX; if (indegree.count(s)) { for(const auto& v : indegree[s]) { int from = v[0]; int price = v[1]; int subProblem = dp(from, k - 1);

if (subProblem != -1) { res = min(res, subProblem + price); } } } // 存入备忘录 memo[s][k] = res == INT_MAX ? -1 : res; return memo[s][k]; } };

python

class Solution: def __init__(self): self.src = 0 self.dst = 0 self.indegree = {} # 备忘录 self.memo = [] def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int: K += 1 self.src = src self.dst = dst # 初始化备忘录，全部填一个特殊值 self.memo = [[-888] * (K + 1) for _ in range(n)] for f in flights: from_, to, price = f if to not in self.indegree: self.indegree[to] = [] self.indegree[to].append([from_, price]) return self.dp(dst, K) # 定义：从 src 出发，k 步之内到达 s 的最小成本 def dp(self, s: int, k: int) -> int: # base case if s == self.src: return 0 if k == 0: return -1 # 查备忘录，防止冗余计算 if self.memo[s][k] != -888: return self.memo[s][k] # 状态转移代码不变 res = float('inf') if s in self.indegree: for v in self.indegree[s]: from_, price = v subProblem = self.dp(from_, k - 1)

if subProblem != -1: res = min(res, subProblem + price) # 存入备忘录 self.memo[s][k] = -1 if res == float('inf') else res return self.memo[s][k]

func findCheapestPrice(n int, flights [][]int, src, dst, K int) int { indegree := make(map[int][][2]int) K++ // 初始化备忘录，全部填一个特殊值 memo := make([][]int, n) for i := range memo { memo[i] = make([]int, K + 1) for j := range memo[i] { memo[i][j] = -888 } } for _, f := range flights { from, to, price := f[0], f[1], f[2] indegree[to] = append(indegree[to], [2]int{from, price}) } return dp(src, dst, K, indegree, memo) } // 定义：从 src 出发，k 步之内到达 s 的最小成本 func dp(src, s, k int, indegree map[int][][2]int, memo [][]int) int { // base case if s == src { return 0 } if k == 0 { return -1 } // 查备忘录，防止冗余计算 if memo[s][k] != -888 { return memo[s][k] } // 状态转移代码不变 res := math.MaxInt32 if v, ok := indegree[s]; ok { for _, p := range v { from, price := p[0], p[1] subProblem := dp(src, from, k - 1, indegree, memo) if subProblem != -1 { res = min(res, subProblem + price) } } } // 存入备忘录 if res == math.MaxInt32 { memo[s][k] = -1 } else { memo[s][k] = res } return memo[s][k] }

javascript

备忘录初始值为啥初始为 -888？前文 base case 和备忘录的初始值怎么定说过，随便初始化一个无意义的值就行。

至此，这道题就通过自顶向下的递归方式解决了。当然，完全可以按照这个解法衍生出自底向上迭代的动态规划解法，但由于篇幅所限，我就不写了，反正本质上都是一样的。

其实，大家如果把之前的所有动态规划文章都看一遍，就会发现我们一直在套用动态规划核心套路，其实真没什么困难的。

最后扩展一下，有的读者可能会问：既然这个问题本质上是一个图的遍历问题，为什么不需要 visited 集合记录已经访问过的节点？

这个问题我在 Dijkstra 算法模板中探讨过，可以去看看。另外，这题也可以利用 Dijkstra 算法模板来解决，代码如下：

java

class Solution { public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) { List<int[]>[] graph = new LinkedList[n]; for (int i = 0; i < n; i++) { graph[i] = new LinkedList<>(); } for (int[] edge : flights) { int from = edge[0]; int to = edge[1]; int price = edge[2]; graph[from].add(new int[]{to, price}); } // 启动 dijkstra 算法 // 计算以 src 为起点在 k 次中转到达 dst 的最短路径 K++; return dijkstra(graph, src, K, dst); } class State { // 图节点的 id int id; // 从 src 节点到当前节点的花费 int costFromSrc; // 从 src 节点到当前节点经过的节点个数 int nodeNumFromSrc; State(int id, int costFromSrc, int nodeNumFromSrc) { this.id = id; this.costFromSrc = costFromSrc; this.nodeNumFromSrc = nodeNumFromSrc; } } // 输入一个起点 src，计算从 src 到其他节点的最短距离 int dijkstra(List<int[]>[] graph, int src, int k, int dst) { // 定义：从起点 src 到达节点 i 的最短路径权重为 distTo[i] int[] distTo = new int[graph.length]; // 定义：从起点 src 到达节点 i 的最小权重路径至少要经过 nodeNumTo[i] 个节点 int[] nodeNumTo = new int[graph.length]; Arrays.fill(distTo, Integer.MAX_VALUE); Arrays.fill(nodeNumTo, Integer.MAX_VALUE); // base case distTo[src] = 0; nodeNumTo[src] = 0; // 优先级队列，costFromSrc 较小的排在前面 Queue<State> pq = new PriorityQueue<>((a, b) -> { return a.costFromSrc - b.costFromSrc; }); // 从起点 src 开始进行 BFS pq.offer(new State(src, 0, 0)); while (!pq.isEmpty()) { State curState = pq.poll(); int curNodeID = curState.id; int costFromSrc = curState.costFromSrc; int curNodeNumFromSrc = curState.nodeNumFromSrc; if (curNodeID == dst) { // 找到最短路径 return costFromSrc; } if (curNodeNumFromSrc == k) { // 中转次数耗尽 continue; } // 将 curNode 的相邻节点装入队列 for (int[] neighbor : graph[curNodeID]) { int nextNodeID = neighbor[0]; int costToNextNode = costFromSrc + neighbor[1]; // 中转次数消耗 1 int nextNodeNumFromSrc = curNodeNumFromSrc + 1; // 更新 dp table if (distTo[nextNodeID] > costToNextNode) { distTo[nextNodeID] = costToNextNode; nodeNumTo[nextNodeID] = nextNodeNumFromSrc; } // 剪枝，如果中转次数更多，花费还更大，那必然不会是最短路径 if (costToNextNode > distTo[nextNodeID] && nextNodeNumFromSrc > nodeNumTo[nextNodeID]) { continue; } pq.offer(new State(nextNodeID, costToNextNode, nextNodeNumFromSrc)); } } return -1; } }

cpp

class Solution { public: struct State { // 图节点的 id int id; // 从 src 节点到当前节点的花费 int costFromSrc; // 从 src 节点到当前节点经过的节点个数 State(int id, int costFromSrc, int nodeNumFromSrc) { this->id = id; this->costFromSrc = costFromSrc; this->nodeNumFromSrc = nodeNumFromSrc; } }; // 自定义比较器，以实现优先队列中costFromSrc较小的元素优先 class CompareState { public: bool operator()(State const& s1, State const& s2) { return s1.costFromSrc > s2.costFromSrc; } }; int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) { vector<vector<int*>> graph(n); for (vector<int> edge : flights) { int from = edge[0]; int to = edge[1]; int price = edge[2]; int* arr = new int[2]{to, price}; graph[from].push_back(arr); } // 启动 dijkstra 算法 // 计算以 src 为起点在 k 次中转到达 dst 的最短路径 K++; return dijkstra(graph, src, K, dst); } int dijkstra(vector<vector<int*>>& graph, int src, int k, int dst) { // 定义：从起点 src 到达节点 i 的最短路径权重为 distTo[i] vector<int> distTo(graph.size(), INT_MAX); // 定义：从起点 src 到达节点 i 的最小权重路径至少要经过 nodeNumTo[i] 个节点 vector<int> nodeNumTo(graph.size(), INT_MAX); // base case distTo[src] = 0; nodeNumTo[src] = 0; // 优先级队列，costFromSrc 较小的排在前面 priority_queue<State, vector<State>, CompareState> pq; // 从起点 src 开始进行 BFS pq.push(State(src, 0, 0)); while (!pq.empty()) { State curState = pq.top(); pq.pop(); int curNodeID = curState.id; int costFromSrc = curState.costFromSrc; int curNodeNumFromSrc = curState.nodeNumFromSrc; if (curNodeID == dst) { // 找到最短路径 return costFromSrc; } if (curNodeNumFromSrc == k) { // 中转次数耗尽 continue; } // 将当前节点相邻节点装入队列 for (int* neighbor : graph[curNodeID]) { int nextNodeID = neighbor[0]; int costToNextNode = costFromSrc + neighbor[1]; // 中转次数消耗 1 int nextNodeNumFromSrc = curNodeNumFromSrc + 1; // 更新 dp table if (distTo[nextNodeID] > costToNextNode) { distTo[nextNodeID] = costToNextNode; nodeNumTo[nextNodeID] = nextNodeNumFromSrc; } // 剪枝，如果中转次数更多，花费还更大，那必然不会是最短路径 if (costToNextNode > distTo[nextNodeID] && nextNodeNumFromSrc > nodeNumTo[nextNodeID]) { continue; } pq.push(State(nextNodeID, costToNextNode, nextNodeNumFromSrc)); } } return -1; } };

python

from heapq import heappop, heappush class State: def __init__(self, id, costFromSrc, nodeNumFromSrc): self.id = id self.costFromSrc = costFromSrc self.nodeNumFromSrc = nodeNumFromSrc def __lt__(self, other): return self.costFromSrc < other.costFromSrc class Solution: def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int: graph = [[] for _ in range(n)] for edge in flights: from_, to, price = edge graph[from_].append([to, price]) # 启动 dijkstra 算法 # 计算以 src 为起点在 k 次中转到达 dst 的最短路径 K += 1 return self.dijkstra(graph, src, K, dst) # 输入一个起点 src，计算从 src 到其他节点的最短距离 def dijkstra(self, graph, src, k, dst): # 定义：从起点 src 到达节点 i 的最短路径权重为 distTo[i] distTo = [float('inf')] * len(graph) # 定义：从起点 src 到达节点 i 的最小权重路径至少要经过 nodeNumTo[i] 个节点 nodeNumTo = [float('inf')] * len(graph) # base case distTo[src] = 0 nodeNumTo[src] = 0 # 优先级队列，costFromSrc 较小的排在前面 pq = [] heappush(pq, State(src, 0, 0)) while pq: curState = heappop(pq) curNodeID = curState.id costFromSrc = curState.costFromSrc curNodeNumFromSrc = curState.nodeNumFromSrc if curNodeID == dst: # 找到最短路径 return costFromSrc if curNodeNumFromSrc == k: # 中转次数耗尽 continue # 将 curNode 的相邻节点装入队列 for neighbor in graph[curNodeID]: nextNodeID, price = neighbor costToNextNode = costFromSrc + price # 中转次数消耗 1 nextNodeNumFromSrc = curNodeNumFromSrc + 1 # 更新 dp table if distTo[nextNodeID] > costToNextNode: distTo[nextNodeID] = costToNextNode nodeNumTo[nextNodeID] = nextNodeNumFromSrc # 剪枝，如果中转次数更多，花费还更大，那必然不会是最短路径 if costToNextNode > distTo[nextNodeID] and nextNodeNumFromSrc > nodeNumTo[nextNodeID]: continue heappush(pq, State(nextNodeID, costToNextNode, nextNodeNumFromSrc)) return -1

import ( "container/heap" "math" ) func findCheapestPrice(n int, flights [][]int, src int, dst int, K int) int { graph := make([][]int, n) for i := 0; i < n; i++ { graph[i] = []int{} } for _, edge := range flights { from := edge[0] to := edge[1] price := edge[2] graph[from] = append(graph[from], to, price) } // 启动 dijkstra 算法 // 计算以 src 为起点在 k 次中转到达 dst 的最短路径 K++ return dijkstra(graph, src, K, dst) } type State struct { id int costFromSrc int nodeNumFromSrc int } // 输入一个起点 src，计算从 src 到其他节点的最短距离 func dijkstra(graph [][]int, src int, k int, dst int) int { // 定义：从起点 src 到达节点 i 的最短路径权重为 distTo[i] distTo := make([]int, len(graph)) // 定义：从起点 src 到达节点 i 的最小权重路径至少要经过 nodeNumTo[i] 个节点 nodeNumTo := make([]int, len(graph)) for i := range distTo { distTo[i] = math.MaxInt } for i := range nodeNumTo { nodeNumTo[i] = math.MaxInt } // base case distTo[src] = 0 nodeNumTo[src] = 0 // 优先级队列，costFromSrc 较小的排在前面 pq := &PriorityQueue{} heap.Push(pq, &State{src, 0, 0}) for pq.Len() > 0 { curState := heap.Pop(pq).(*State) curNodeID := curState.id costFromSrc := curState.costFromSrc curNodeNumFromSrc := curState.nodeNumFromSrc if curNodeID == dst { // 找到最短路径 return costFromSrc } if curNodeNumFromSrc == k { // 中转次数耗尽 continue } // 将 curNode 的相邻节点装入队列 for i := 0; i < len(graph[curNodeID]); i += 2 { nextNodeID := graph[curNodeID][i] costToNextNode := costFromSrc + graph[curNodeID][i+1] // 中转次数消耗 1 nextNodeNumFromSrc := curNodeNumFromSrc + 1 // 更新 dp table if distTo[nextNodeID] > costToNextNode { distTo[nextNodeID] = costToNextNode nodeNumTo[nextNodeID] = nextNodeNumFromSrc } // 剪枝，如果中转次数更多，花费还更大，那必然不会是最短路径 if costToNextNode > distTo[nextNodeID] && nextNodeNumFromSrc > nodeNumTo[nextNodeID] { continue } heap.Push(pq, &State{nextNodeID, costToNextNode, nextNodeNumFromSrc}) } } return -1 } type PriorityQueue []*State func (pq PriorityQueue) Len() int { return len(pq) } func (pq PriorityQueue) Less(i, j int) bool { return pq[i].costFromSrc < pq[j].costFromSrc } func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] } func (pq *PriorityQueue) Push(x interface{}) { *pq = append(*pq, x.(*State)) } func (pq *PriorityQueue) Pop() interface{} { old := *pq n := len(old) item := old[n-1] *pq = old[0 : n-1] return item }

javascript

关于这个解法这里就不多解释了，可对照前文 Dijkstra 算法模板理解。

引用本文的题目

安装我的 Chrome 刷题插件点开下列题目可直接查看解题思路：

LeetCode力扣难度286. Walls and Gates286. 墙与门