最速下降法及案例分析(含MATLAB代码)

案例研究：分析成功案例，学习最佳实践。 #生活常识# #职场技巧# #知识更新#

这里介绍的主要是二维的案例 一、最速下降法的背景与应用二、最速下降法的基本原理最速下降法案例分析 四、最速下降法与梯度下降法的区别五、 最速下降法的缺点案例分析的代码

一、最速下降法的背景与应用

最速下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。1

二、最速下降法的基本原理

对于给定的函数 f ( x ) f(x) f(x)由泰勒展开得： f ( x ) = f ( x 0 ) + ∇ f ( x ) ( x − x 0 ) + ∇ f ( x ) ( x − x 0 ) 2 ! + . . . (1) f(x)=f(x_0)+\nabla f(x)(x-x_0)+\frac{\nabla f(x)(x-x_0)}{2!}+... \tag{1} f(x)=f(x0​)+∇f(x)(x−x0​)+2!∇f(x)(x−x0​)​+...(1)取它的第二阶展开，则 f ( x ) ≈ f ( x 0 ) + ∇ f ( x ) ( x − x 0 ) (2) f(x)\approx f(x_0)+\nabla f(x)(x-x_0) \tag{2} f(x)≈f(x0​)+∇f(x)(x−x0​)(2)

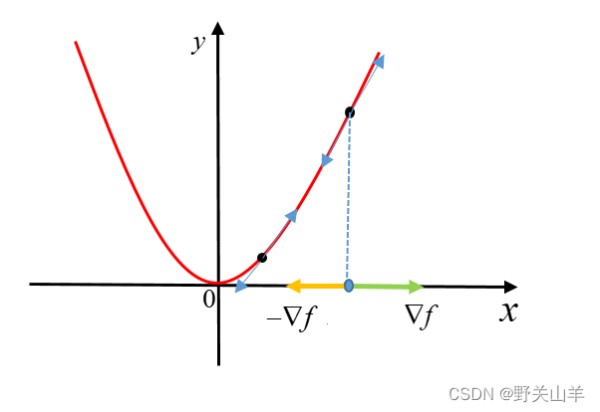
如上图所示 ∇ f \nabla f ∇f为梯度方向， − ∇ f -\nabla f −∇f为负梯度方向(反向梯度)。所以我们就有 x − x 0 = − α ∗ ∇ f ( x 0 ) (3) x-x_0=-\alpha *\nabla f(x_0)\tag{3} x−x0​=−α∗∇f(x0​)(3)那么就得到迭代公式 x k + 1 = x k − α ∗ ∇ f ( x k ) , ( α > 0 ) (4) x_{k+1}=x_k-\alpha *\nabla f(x_k),(\alpha>0)\tag{4} xk+1​=xk​−α∗∇f(xk​),(α>0)(4)
其中 α \alpha α称为学习率。也可以理解为步长， α \alpha α的不同，会导致迭代次数不同，收敛速度就不同。

最速下降法案例分析

下面取一个例子 f ( x ) = x 2 f(x)=x^2 f(x)=x2, ∇ f ( x ) = 2 x \nabla f(x)=2x ∇f(x)=2x, x 0 = 10 , α = 0.2 x_0=10,\alpha=0.2 x0​=10,α=0.2由迭代公式(4)有：

x k {x_k} xk​ x k + 1 = x k − α ∗ ∇ f ( x k ) x_{k+1}=x_k-\alpha *\nabla f(x_k) xk+1​=xk​−α∗∇f(xk​) ∇ f ( x k ) \nabla f(x_k) ∇f(xk​) x 1 x_1 x1​ x 1 = x 0 − α ∗ ∇ f ( x 0 ) = 6 x_1=x_0-\alpha *\nabla f(x_0)=6 x1​=x0​−α∗∇f(x0​)=6 ∇ f ( x 1 ) \nabla f(x_1) ∇f(x1​)=12 x 2 x_2 x2​ x 2 = x 1 − α ∗ ∇ f ( x 1 ) = 3.6 x_2=x_1-\alpha *\nabla f(x_1)=3.6 x2​=x1​−α∗∇f(x1​)=3.6 ∇ f ( x 2 ) \nabla f(x_2) ∇f(x2​)=7.2 x 3 x_3 x3​ x 3 = x 2 − α ∗ ∇ f ( x 2 ) = 2.16 x_3=x_2-\alpha *\nabla f(x_2)=2.16 x3​=x2​−α∗∇f(x2​)=2.16 ∇ f ( x 3 ) \nabla f(x_3) ∇f(x3​)=4.32………

按照这样迭代下去，只要给定一个精度值 ϵ \epsilon ϵ,使得 ∇ f ( x k ) \nabla f(x_k) ∇f(xk​)< ϵ \epsilon ϵ,就可以了。如下图，它是越来越靠近最低点的。

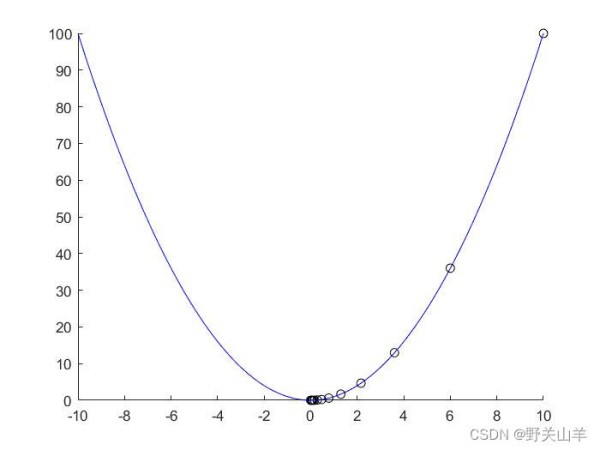
通过观察下这个图可以看到，学习率 α \alpha α取的不同，迭代次数也会不同，选择合适的学习率，收敛速度会更快。

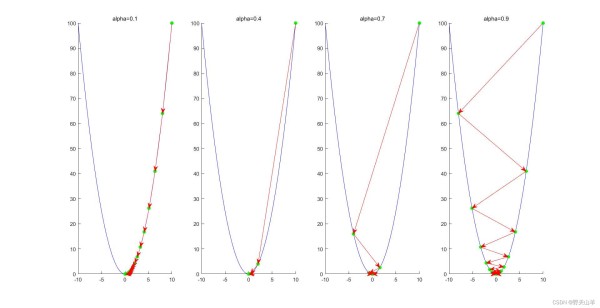
四、最速下降法与梯度下降法的区别

最速下降法与梯度下降法的主要区别在最速下降法有学习率 α \alpha α，而梯度下降法没有(就是 α \alpha α恒等等于1，是不变的)，梯度下降法默认负梯度方向就是目标函数值下降最快的方向。即 △ x = − ∇ f ( x ) \triangle x=-\nabla f(x) △x=−∇f(x),故每次都将自变量沿着负梯度方向移动单位步长，目标函数值就会逐渐收敛。但是收敛速度非常大的程度地依赖于其Hessian矩阵的条件数2。

五、 最速下降法的缺点

某点的负梯度方向，通常只是在该点附近才具有这种最速下降的性质。在一般情况下，当用最速下降法寻找极小点时，在开始几步目标函数下降较快；但在接近极小点时，收敛速度长久不理想了。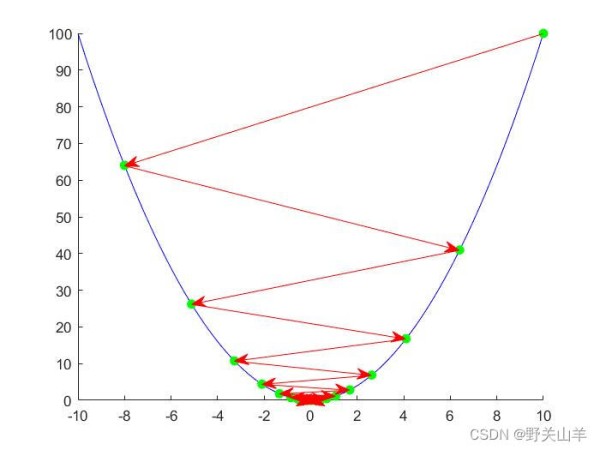
通过上面案例分析也可以清晰的看到，在开始时都是收敛比较快(图像上的点比较稀疏)，而在靠近极小值时，收敛比较慢。从图像是上看密密麻麻的。如果当目标函数的等值 线为比较扁平的椭圆时，那收敛就更慢了。所以，在实用中常用最速下降法和其他方法联合应用，在前期使用最速下降法，而在接近极小值点时，可以改用收敛较快的其他方法。
还有就是最速下降法只能得到局部最优，也就是说当你的函数有多个极值时。函数值是否最小与于初始值 x 0 x_0 x0​的选举有关。

案例分析的代码

clear,clc %f=x^2;%df=2*x; x0=15; %初始值 el=0.0001; %设置精度 n=0.9; %学习率 x1=x0-n*2*x0; k=1; while abs(2*x1)>el x0=x1; x1=x0-n*2*x0; k=k+1; %k为迭代次数 end xd=2*x1 k %%%%%%%%%%%%%%%%%%%%%%下面是给图像标箭头 while abs(2*x1)>el x0=x1; x1=x0-n*2*x0; k=k+1; %k为迭代次数 end xd=2*x1 k x11(1)=10; for i=1:k x11(i+1)=x11(i)-n*2*x11(i); end x11 y=x11.^2 scatter(x11,y,'k') hold on t=-10:0.01:10; y1=t.^2; plot(t,y1,'b') for i=1:k PlotLineArrow(gca,[x11(i),x11(i+1)],[y(i),y(i+1)],'g','r') end

1234567891011121314151617181920212223242526272829303132333435

下面是画箭头的m.文件3。

function PlotLineArrow(obj, x, y, markerColor, lineColor) % 绘制带箭头的曲线 % 绘制散点图 plot(x, y, 'o', 'Color', markerColor, 'MarkerFaceColor', markerColor); % 获取 Axes 位置 posAxes = get(obj, 'Position'); posX = posAxes(1); posY = posAxes(2); width = posAxes(3); height = posAxes(4); % 获取 Axes 范围 limX = get(obj, 'Xlim'); limY = get(obj, 'Ylim'); minX = limX(1); maxX = limX(2); minY = limY(1); maxY = limY(2); % 转换坐标 xNew = posX + (x - minX) / (maxX - minX) * width; yNew = posY + (y - minY) / (maxY - minY) * height; % 画箭头 annotation('arrow', xNew, yNew, 'color', lineColor);

123456789101112131415161718192021

来自百度百科 ↩︎

来自知乎作者为“一土木蒙” ↩︎

来自CSDN的作者CoderMan_1012 ↩︎

网址：最速下降法及案例分析(含MATLAB代码) https://www.yuejiaxmz.com/news/view/398848

相关内容

Matlab代码实践——BP神经网络
【负荷预测】基于DBO、PSO、SSA、GOOSE算法优化ELM的电力负荷预测研究附Matlab代码
PCA （主成分分析）详解 （写给初学者） 结合matlab
MATLAB图像处理（包括图像类型转换）
【创新未发表】基于鱼鹰OOA求解带时间窗的骑手外卖配送路径规划问题，最优路径成本附Matlab代码
【优化调度】基于多时间尺度的电动汽车光伏充电站联合分层优化调度附Matlab代码
Matlab 透视变换原理 代码实现
情感融入之语音识别原理及应用（包含实例代码）
【Matlab 六自由度机器人】关于灵活工作空间与可达工作空间的理解（附MATLAB推导代码）
matlab中for循环的简单使用

随便看看