最近在看一篇论文《Learning Latent Opinions for Aspect-Level Sentiment Classification》里面用到了条件随机场以及BiLSTM模型,以此记录。
主要是基于李航的《统计学习方法》一书加上自己的见解最后总结得出:
首先,要理解一个概念:概率无向图模型。
概率无向图模型定义:设有联合概率分布P(Y),由无向图G=(V,E)表示,在图G中,节点表示随机变量,边表示随机变量之间的依赖关系。如果联合概率分布P(Y)满足成对、局部或者全局马尔科夫性,就称此联合概率分布为概率无向图模型或马尔可夫随机场。
这句话中包含几个定义:联合概率;无向图;成对、局部或者全局马尔科夫性。
联合概率和无向图的定义在这里就不解释了,主要解释下马尔科夫性。
成对马尔可夫性:
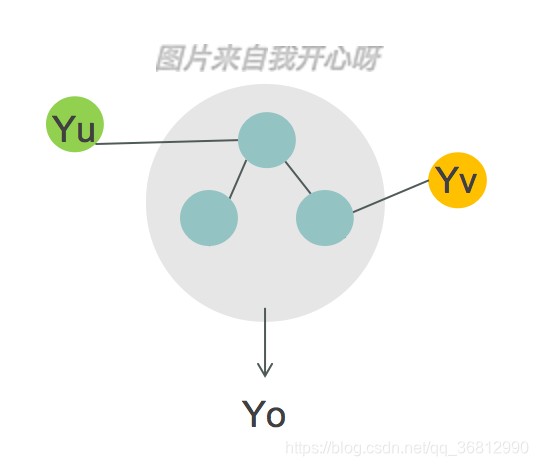
设u和v是无向图G中任意两个没有边连接的结点,节点u和v分别对应随机向量Yu和Yv;其他所有节点为O,对应的随机变量组是Yo;
成对马尔可夫性指给定随机变量组Yo的条件下随机变量Yu和Yv是条件独立的。即:
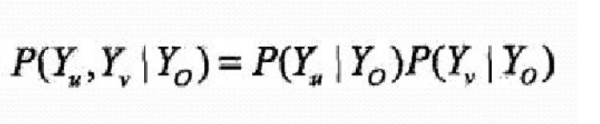
局部马尔科夫性:
设v是无向图G中任一结点,W是与v有边连接的所有结点,O是v,W以外的其他所有节点。v表示的随机变量是Yv,W表示的随机变量组是Yw,O表示的随机变量组是Yo。局部马尔科夫性是指在给定随机变量组Yw的条件下随机变量Yv与随机变量Yo是独立的,即:
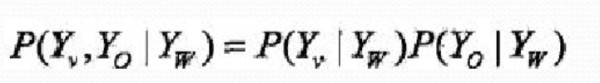

 我开心呀 于 2019-11-01 21:36:23 发布
我开心呀 于 2019-11-01 21:36:23 发布
