简介
探讨优化等级与运行效率关系.
简单加法运算
测试平台 STM32F407(时钟168MHz)Zynq 7z020(单核)Intel i5-4590 CPU @3.3GHz 3.3GHz 测试核心代码::
void add(u32 N); void test_add(void) {u32 N=100000;while(N-->0){add(100000);}return; } void add(u32 N) {u32 a=0, b=0;while(N-- > 0){a = b+N;} }
12345678910111213141516171819202122 测试结果下图为STM32F407 运行记录
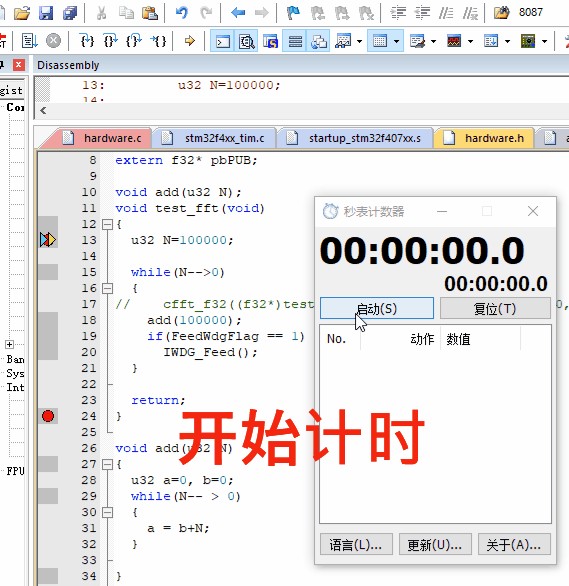
下图为ZYNQ 7Z020 运行记录
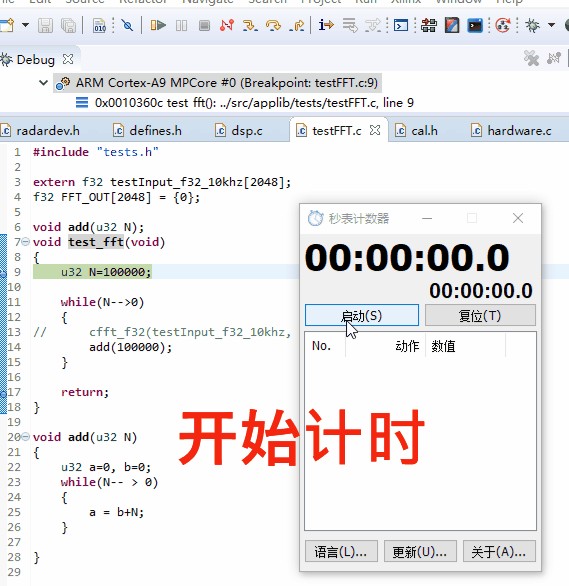
下图为Intel i5-4590 运行记录
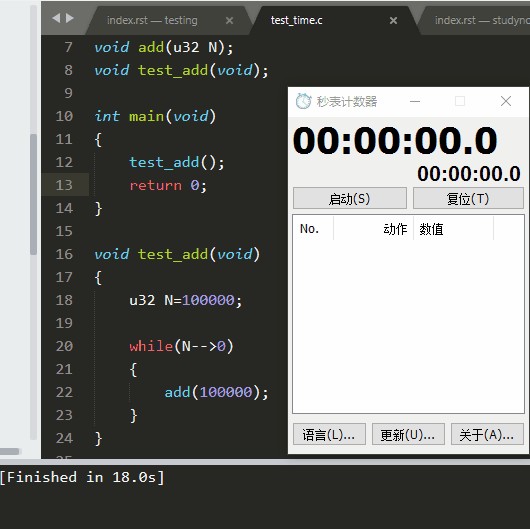
下图给出了各平台运算时间效率对比结果图
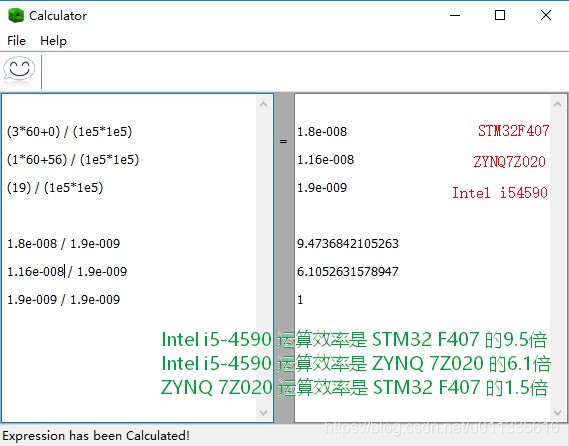
快速傅里叶变换
测试平台 STM32F407(时钟168MHz)Zynq 7z020(单核) 测试核心代码::
void invert(complex32 *pSrc, u32 n) {int *a, i, j, w, t;complex32 tc;a = (int*)malloc(sizeof(int)*n);for (i = 0; i < n; i++)a[i] = i;w = n / 2;j = n / 2;for (i = 1; i<n - 1; i++){if (a[i] != j){t = a[j]; a[j] = a[i]; a[i] = t;tc = pSrc[j];pSrc[j] = pSrc[i];pSrc[i] = tc;}w = n / 2;while (j >= w)j = j - w, w = w / 2;j = j + w;}free(a); } void fft32(complex32 *pSrc, u32 n) {u32 kn, k, a, b, c, d, e, i, i1, i2;complex32 *Wn, x1, x2;invert(pSrc, n);Wn = (complex32*)malloc(sizeof(complex32)*n / 2);for (i = 0; i<n / 2; i++){Wn[i].real = cos(2 * PI*i / n);Wn[i].imag = -sqrt(1 - (Wn[i].real*Wn[i].real));}kn = log2(n);b = 1; a = n / 2; c = 2;for (k = 0; k<kn; k++){for (d = 0; d<a; d++)for (e = 0; e<b; e++){i1 = c * d + e; i2 = i1 + b;x1 = pSrc[i1];x2.real = pSrc[i2].real*Wn[e*a].real - pSrc[i2].imag*Wn[e*a].imag;x2.imag = pSrc[i2].real*Wn[e*a].imag + pSrc[i2].imag*Wn[e*a].real;pSrc[i1].real = x1.real + x2.real;pSrc[i1].imag = x1.imag + x2.imag;pSrc[i2].real = x1.real - x2.real;pSrc[i2].imag = x1.imag - x2.imag;}b = b * 2; a = a / 2; c = c * 2;}free(Wn); }
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758 测试结果1024点, float32型FFT, 运行100000, 取平均.
STM32F407(时钟168MHz, 上述代码): 21.4ms, 优化等级为3Zynq 7z020(单核, 上述代码): 2.2ms, 无优化STM32F407(时钟168MHz, STM32官方库): 0.78ms, 优化等级为3Zynq 7z020(单核, STM32官方库): 0.71ms, 无优化Zynq 7z020(单核, STM32官方库): 0.23ms, 优化等级为3Zynq 7z020(单核, Ne10): 0.7ms编译优化等级的影响
测试平台 STM32F407(时钟168MHz)Zynq 7z020(单核) 测试核心代码上述代码
测试结果 平台: STM32F407(时钟168MHz) 对较简单的加法(1e10次) 优化等级0: 300s优化等级3: 180s 对较复杂的FFT(1e4次, 上述复杂程序) 优化等级0: 217s优化等级3: 214s 平台: Zynq 7z020(单核) 对较简单的加法(1e10次) 优化等级0: 300s优化等级3: 180s 对较复杂的FFT(1e5次, STM32官方库) 优化等级0: 71.2s优化等级3: 22.9s可见优化等级越高, 运行效率越高, 特别地, 对于上述加法, 由于 a 仅在 a = b+N 中被使用, 所以可以省去赋值操作, 因而优化等级高时, 会将此优化, 因而运算效率差距明显. 对于较复杂的算法, 如果程序中不存在冗余无用的代码, 优化前后, 应该相差不大.
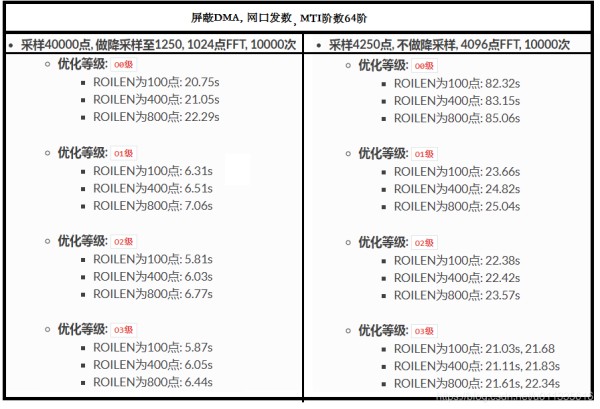
结论:
优化等级为O0 与 O1~O3时相比, 运行时间相差较大;优化等级为O1, O2, O3时相比, 运行时间相差不大;

