分治法：从图片压缩到快速幂，揭秘“分而治之”的高效算法

快速烹饪：早餐三明治的做法 #生活乐趣# #生活分享# #生活技能教学# #美食制作分享#

一招破解复杂问题：分解、解决、合并的智慧

一. 从一个生活场景开始：手机照片压缩

现代智能手机的相机像素越来越高，单张照片大小可达2-3MB。在上传或分享时，大文件不仅耗费流量，还会增加等待时间。传统的全局压缩方法往往会导致图片严重失真，而分治法提供了更科学的解决方案。

核心压缩流程：

分：将整张图片拆分为多个小像素块（如4×4子块）治：对每个子块计算平均色值，进行简化压缩并：合并所有子块，生成压缩后的图片

具体实现时，首先对图片进行“缩”处理，根据宽高比例进行尺寸压缩，然后再进行“压”处理，根据文件大小调整压缩系数。这种方法基于图片的局部特征进行优化，能更好地保持图片质量。

二. 分治法的核心思想：化繁为简的艺术

分治法是算法设计中的核心方法，其核心思想是将复杂问题分解为多个相同或相似的子问题，通过递归求解并合并结果以获得原问题的解。

2.1 分治法的三个步骤

分解：将原问题分解为多个子问题。这些子问题应该是同类的，规模更小的问题。解决：递归求解各子问题。如果子问题足够小，则直接求解。合并：将子问题的解合并为原问题的解。

2.2 分治法适用的情况

问题可分解性：问题可以分解为规模更小、类似的子问题子问题独立性：子问题之间不包含公共的子问题解可合并性：子问题的解可以合并为原问题的解

三. 分治法的经典应用：快速幂算法

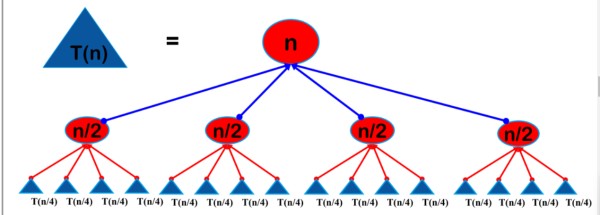
快速幂算法是分治法的典型应用，用于高效计算a的n次方，其时间复杂度为O(log₂N)，与朴素的O(N)相比效率有了极大的提高。代码如下

#include <iostream>

#include <ctime>

using namespace std;

double iter_pow(double a,int n)

{

int i;

double result=1;

for(i=0;i<n;i++)

{

result=result*a;

}

return result;

}

double recur_pow(double a,int n)

{

if(n == 0) return 1;

return a*recur_pow(a,n-1);

}

double dc_pow_adv(double a,int n)

{

if(n == 0) return 1;

double half = dc_pow_adv(a, n / 2);

if (n % 2 == 0)

{

return half * half;

}

else

{

return half * half * a;

}

}

int main()

{

double a,result;

int start,end,t,n,i;

a=1.01;

cout<<"请输入n计算1.01^n：";

cin>>n;

start=clock();

for(i=0;i<10000;i++)

result=iter_pow(a,n);

end=clock();

t=end-start;

cout<<"递推求快速幂结果:"<<result<<endl<<"耗费时间:"<<t<<"ms"<<endl;

start=clock();

for(i=0;i<10000;i++)

result=recur_pow(a,n);

end=clock();

t=end-start;

cout<<"递归求快速幂结果:"<<result<<endl<<"耗费时间:"<<t<<"ms"<<endl;

start=clock();

for(i=0;i<10000;i++)

result=dc_pow(a,n);

end=clock();

t=end-start;

cout<<"分治法求快速幂结果:"<<result<<endl<<"耗费时间:"<<t<<"ms"<<endl;

start=clock();

for(i=0;i<10000;i++)

result=dc_pow_adv(a,n);

end=clock();

t=end-start;

cout<<"改进分治法求快速幂结果:"<<result<<endl<<"耗费时间:"<<t<<"ms"<<endl;

return 0;

}

cs

运行

3.2 算法分析

传统方法：需要n-1次乘法，时间复杂度O(n)快速幂算法：每次将问题规模减半，时间复杂度O(log n)

当n=10000时，快速幂算法仅需约14次递归调用，而传统方法需要10000次乘法，效率提升显著。

四. 分治法的另一应用：二分搜索算法

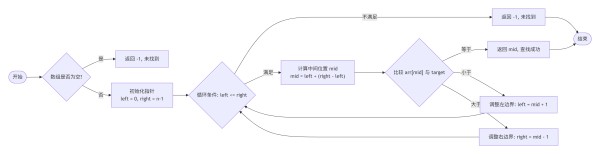
二分搜索是分治法在查找领域的经典应用，适用于有序序列。

4.1 算法实现

#include <iostream>

#include <ctime>

using namespace std;

int BinSearch(int a[],int low,int high,int key)

{

if (low<=high)

{

int mid = (low+high)/2;

if(a[mid] == key)

return mid;

else if(key<a[mid])

return BinSearch(a, low, mid - 1, key);

else if(key>a[mid])

return BinSearch(a, mid + 1, high, key);

}

else

return -1;

}

int main()

{

int a[10]={1,2,3,4,5,6,7,8,9,10};

cout<<"key1在a["<<BinSearch(a,0,9,9)<<"]中存储"<<endl;

cout<<"key2在a["<<BinSearch(a,0,9,1)<<"]中存储"<<endl;

cout<<"key3在a["<<BinSearch(a,0,9,5)<<"]中存储"<<endl;

return 0;

}

cs

运行

4.2 算法分析

传统顺序查找：时间复杂度O(n)二分搜索：每次将搜索范围减半，时间复杂度O(log n)

五. 分治法的更多应用场景

分治法在计算机科学领域有广泛应用，以下是一些经典案例：

5.1 排序算法

归并排序：完全遵循分治法思想，将数组递归分割然后合并快速排序：选择基准元素进行分区，然后递归排序

5.2 几何问题

最近点对问题：将点集分割成子集，分别求解后再合并结果凸包问题：利用分治法求解平面点集的凸包

5.3 数学计算

大整数乘法：将大整数分解为小整数进行计算矩阵乘法：Strassen算法通过分治策略降低矩阵乘法的时间复杂度

六. 分治法的优化策略

递归转迭代：消除函数调用栈开销，规避栈溢出避免重复计算：存储已求解子问题结果平衡分割：尽量将问题分解为规模相近的子问题位运算优化：利用位运算提高效率

七. 总结

分治法通过"分而治之，合而为一"的策略，将复杂问题转化为一系列简单子问题，是算法设计中的重要范式。从技术层面的快速幂计算、图片压缩，到生活实践中的任务管理，分治思维都能提供有效的解决问题的框架。

掌握分治法不仅有助于我们成为更好的程序员，更能培养我们系统化、结构化的思维方式，在面对复杂挑战时能够保持清晰的思路和高效的执行力。

欢迎在评论区分享你对分治法的理解和使用经验！如果你有其他有趣的分治法应用案例，也欢迎一起交流讨论。

网址：分治法：从图片压缩到快速幂，揭秘“分而治之”的高效算法 https://www.yuejiaxmz.com/news/view/1418590

相关内容

破解生活难题，揭秘分治算法的智慧应用：从日常琐事到专业挑战，看算法如何简化复杂问题！
揭秘速算秘诀：掌握思维速算法，轻松解锁学习与生活中的高效计算之道！
治便秘的快速与高效策略：自然疗法与生活习惯调整
揭秘46乘以15双倍算法：快速计算秘诀，告别繁琐计算！
EZW算法优化：一种提升图像压缩效率的新方法
揭秘快速去除纹身的高效方法与技巧
根号2的精确值计算与快速幂算法
揭秘日常生活中的算法应用：从购物推荐到智能助手，揭秘你每天都在使用的神秘算法！
c++算法之基本算法篇
揭秘丝滑压缩技巧，轻松玩转高效生活

随便看看