关于C语言中的函数递归与迭代

Swift编程语言：掌握基本语法和函数定义 #生活知识# #编程教程#

首先，什么是递归？

    C语言中的函数是可以调用自己本身的，当我们通过函数的自身调用解决问题时，这种方法被称为递归，它是一种编程技巧。其核心思想就是把一个规模较大的问题拆分成一个个规模更小但逻辑相同的子问题，直到子问题无法再拆分（这就是递归的终止条件），最后由子问题的解一步步推导出原问题的解。这个拆分的过程就是函数的一次次自身调用，传递各自的参数，这就是向下“递”的过程。当“递”到不能再向下了，即子问题拆分到不能再分，此时开始自下而上地向原问题推导，这就是“归”。

我们接下来看一个简单的关于C语言递归的代码。

#include <stdio.h>

int main()

{

printf("1") ;

main() ;

return 0 ;

}

cpp

运行

    在这串代码中，main函数会调用自己，每次调用都会进行一次输出，且由于没有设置终止条件，运行之后它将会陷入死递归，开始不停地打印“1”。但如果我们稍等一会，我们会发现，这个程序最终会停下。为什么呢？因为当程序走起来之后，每次调用main函数，都要占用一部分空间，这里的空间也就是函数栈帧空间，当调用次数一直在增加，栈区最终被占满，就会导致栈溢出，程序因此被迫停下。

    这串代码虽然是错误的，但是它让我们切实感受到了函数的自身调用，并且提醒我们，为了不让函数无限递归，递归必须是有条件的。

    C语言函数递归的核心思想就是把一个规模较大的问题拆分成一个个规模更小但逻辑相同的子问题，直到子问题无法再拆分（这就是递归的终止条件），最后由子问题的解一步步推导出原问题的解。这个拆分的过程就是函数的一次次自身调用，传递各自的参数，这就是向下“递”的过程。当“递”到不能再向下了，即子问题拆分到不能再分，此时开始自下而上地向原问题推导，这就是“归”。

    接下来我们看一个问题：“求正整数n的阶乘”。如何用函数递归去解决呢？我们不妨回归递归的核心思想，求n！则可以拆分为求 n*(n-1)! ，那求(n-1)!又可以拆分成求 (n-1)*(n-2)! ,以此类推，最后我们可以将问题拆到2*1,1不能再拆了，便由此回推到原问题。写成代码如下:

#include <stdio.h>

int Fac (int n)

{

if (n == 1)

{

return 1 ;

}

else

{

return n * Fac(n-1) ;

}

}

int main()

{

int n = 0 ;

scanf("%d",&n) ;

printf("%d",Fac(n)) ;

return 0 ;

}

cpp

运行

  由此我们可以总结一下使用递归的两个必须要求：

     1. 递归存在终止条件（限制条件），当满足该条件时，函数不再进行自身调用 。

     2. 函数每次的自身调用都要逐渐去接近递归的终止条件。

  这样，我们才能保证写出的函数不会陷入死递归 。

    那我们紧接着，我们根据这两个必须要求，再来看一个问题 ：“顺序输出正整数n的各位数字”。一样的，我们去思考怎么把这个问题拆成简单的子问题。因为我们可以通过1234%10来得到4 ，那我们是不是就可以先顺序输出123的个位数字再输出这个4？以此类推，对于123我们可以先顺序输出12的个位数字再输出3 ，最后我们只需要输出单独的首位数字1 ，接着输出2 。顺着这个思路，我们就可以写出以下代码：

#include <stdio.h>

void Print (int n)

{

if (n / 10 == 0)

{

printf("%d ",n%10) ;

}

else

{

Print(n/10) ;

printf("%d ",n%10) ;

}

}

int main()

{

int n = 0 ;

scanf("%d",&n) ;

Print(n) ;

return 0 ;

}

cpp

运行

当然我们不难发现，在Print函数中，无论if的条件是否满足，都要执行：

printf("%d ",n%10) ;

cpp

运行

那我们据此可以把Print函数简化一下：

void Print (int n)

{

if (n > 9)

{

Print(n/10) ;

}

printf("%d ",n%10) ;

}

cpp

运行

这样，问题就被我们通过递归巧妙解决了。

    我们不难察觉到，通过递归写出的代码，看起来很简洁。那是不是递归就是完美的呢？答案是否定的。从我们最开始写的那串代码就看出来了，函数的每次调用都要占用一份内存空间，所以当我们递归的层次比较深时，递归在内存上的开销较大 ，甚至也有可能导致栈溢出。

此时，我们就要用迭代来解决问题。迭代通常就是循环的方式。比如，同样是求n的阶乘，我们用迭代的方法写下来就是这样：

#include <stdio.h>

int Fac(int n)

{

int i = 1 ;

int ret = 1 ;

for (i = 1 ; i <= n ; i++)

{

ret *= i ;

}

return ret ;

}

int main()

{

int n = 0 ;

scanf("%d",&n) ;

printf("%d",Fac(n)) ;

return 0 ;

}

cpp

运行

这样我们用迭代也解决了问题 ，且效率更高 。

    我们生活中的很多问题都可以用递归的形式来解释，但可能只是因为用递归的表示更清晰，实际上使用非递归的方式可能更合适 。比如我们想求第n个斐波那契数，

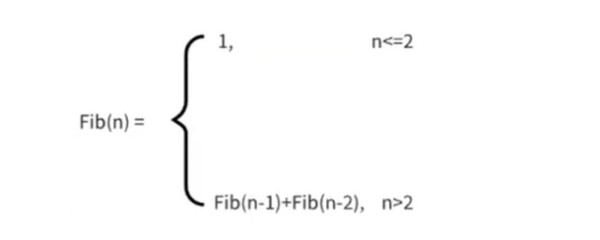
我们一眼就能联想到递归 ，很快就能把代码写出来：

#include <stdio.h>

int Fib (int n)

{

if (n <= 2)

{

return 1 ;

}

else

{

return Fib(n-1) + Fib(n-2) ;

}

}

int main()

{

int n = 0 ;

scanf("%d",&n) ;

printf("%d",Fib(n)) ;

return 0 ;

}

cpp

运行

    当我们输入5时，得到的是5，答案是正确的。但是当我们输入50的时候，我们就会发现问题，程序会跑很长时间，为什么呢？我们可以设置一个全局变量e，每次调用函数都执行一次e++，来观察这个过程到底调用了多少次Fib函数。我们惊奇地发现，当我们要求第50个斐波那契数时，e的值已经过大而输出为负数，当我们输入改为30时

    发现Fib函数竟然被调用了1664079次。所以递归在运行上造成了极大地开销，使得代码效率变低。那我们如果用迭代该怎么写呢？很简单，斐波那契数列的前两个数都是1，后面的数都是前两个数的和：

#include <stdio.h>

int Fib (int n)

{

int a = 1 ;

int b = 1 ;

int c = 0 ;

int i = 0 ;

for (i = 0 ; i < n-2 ; i++)

{

c = a+b ;

int e = a ;

a = b ;

b = c ;

}

return c ;

}

int main()

{

int n = 0 ;

scanf("%d",&n) ;

printf("%d\n",Fib(n)) ;

return 0 ;

}

cpp

运行

    我们会发现使用迭代解决这个问题，程序的效率会高很多。另外，针对这个问题，我们还可以把它看作是兔子繁殖问题：

 “有一对兔子，从出生后第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子。按此规律，假设没有兔子死亡，第一个月有一对刚出生的小兔子，问第n个月有多少对兔子？”

那我们可以试着把能生育和不能生育的兔子分开算，最后合并。

#include <stdio.h>

int Fib (int n)

{

n = n-1 ;

int a = 1 ;

int b = 0 ;

while(n--)

{

int e = a ;

a = b ;

b += e ;

}

return a+b ;

}

int main()

{

int n = 0 ;

scanf("%d",&n) ;

printf("%d\n",Fib(n)) ;

}

cpp

运行

两种迭代的思路都能很好地解决这个问题。那我们究竟什么时候去用递归呢？

    其实我们前面就提到了，递归写出来的代码看起来很简洁。有时候递归几行就解决的问题，如果用非递归的方法，可能要写十几行甚至数十行。所以在某些不是很复杂的场景下，递归的简洁性可以弥补它运行开销较大的缺点 。当然这也考验我们能否针对问题写出简洁且高效的递归 ，所以这都需要我们通过一步步积累和练习，提升自己写出优秀代码的能力。在递归与迭代之间权衡利弊，这不仅是写代码的决策 ，更是我们日常看待问题时的一种生活态度 ！

网址：关于C语言中的函数递归与迭代 https://www.yuejiaxmz.com/news/view/1422952

相关内容

【C语言入门】显式传递数组长度参数
如何优化PHP代码中的循环和递归操作？
【C++ 函数设计的艺术】深挖 C++ 函数参数的选择 智能指针与 std::optional：最佳实践与陷阱
【宝藏系列】嵌入式 C 语言代码优化技巧【超详细版】
递归思想——关于递归的多个例子详解
C语言程序优化工作流程的注意事项
从“数学归纳法”到理解“递归算法”！
递归优化技巧
c语言时间超限求优化
python中关于迭代器的使用

随便看看