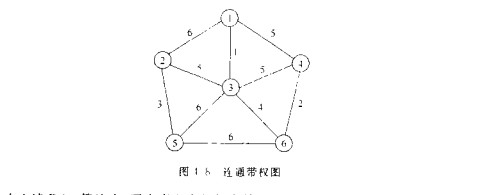
问题描述:
设G = (V, E) 是无向连通带权图, 即一个网络。E的每条边(v, w)的权为c[v][w]。如果G的一个子图G1是一棵包含G所有顶点的树,则称G1为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中,耗费最小的生成树称为G的最小生成树。
解法:
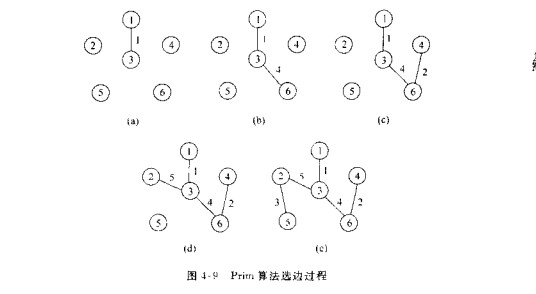
1:Prim算法
思路:设U为已并入最小生成树中的顶点集合,最初任选一点放入U,之后找U到V-U中的最小边,将对应新顶点并入,共N-1轮即可
具体操作:
①从顶点u0开始,令U={u0}, 初始化u0到其余各顶点距离
②找最小边输出,将最小的点并入新顶点, 并将其值赋为0
③更新表
④重复n-1次
代码:
#include <bits/stdc++.h>
using namespace std;
const int max_ = 0x3f3f3f;
int Graph[110][110];
int visited[110];
int closest[110];
int prepos[110];
int pointnum, edgenum;
int FindMinLen()
{
int pos, min_ = max_;
for(int i = 1; i <= pointnum; ++i)
if(min_ > closest[i] && closest[i])
{
min_ = closest[i];
pos = i;
}
return pos;
}
void Prim()
{
for(int i = 2; i <= pointnum; ++i)
{
closest[i] = Graph[1][i];
prepos[i] = 1;
}
closest[1] = 0;
for(int i = 1; i < pointnum; ++i)
{
int pos;
pos = FindMinLen();
closest[pos] = 0;
for(int j = 2; j <= pointnum; ++j)
{
if(closest[j] > Graph[pos][j])
{
closest[j] = Graph[pos][j];
prepos[j] = pos;
}
}
printf("%d -> %d\n", prepos[pos], pos);
}
}
void InPut()
{
int pos1, pos2, len;
scanf("%d %d", &pointnum, &edgenum);
memset(Graph, max_, sizeof(Graph));
for(int i = 1; i <= edgenum; ++i)
{
scanf("%d %d %d", &pos1, &pos2, &len);
Graph[pos1][pos2] = len;
Graph[pos2][pos1] = len;
}
}
int main()
{
InPut();
Prim();
}
输入:
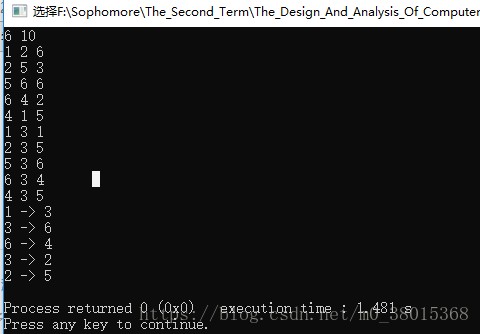
6 10
1 2 6
2 5 3
5 6 6
6 4 2
4 1 5
1 3 1
2 3 5
5 3 6
6 3 4
4 3 5
输出:
1 -> 3
3 -> 6
6 -> 4
3 -> 2
2 -> 5
截图: