递归及典型应用

公园的健身器材使用后应及时归位 #生活知识# #社会生活# #公共设施使用#

递归是一种方法调用自身的编程技术。数学本质是数学归纳方法。接下来我们介绍一些典型的递归应用案例，用以帮助理解，欢迎批评指正。
1.三角数字
　　古希腊数学家发现数字1，3，6，10，15，21，….中存在一种联系。及这个数列中第n项是由第n-1项加n得到，n>1。这个序列中的数字被称为三角数字，因为它们可以被形象化地表示成对象的一个三角排列。
　　

　　
　　图1 三角数字
　　

　　由图1可以很容易看出这些数字的规律，即第n项的值可以被看成只是两个部分的和，分别是：
　　1>第一列，值为n；
　　2>所有剩余列的和。
　　代码如下：

import java.io.*; public class Triangle { public static void main(String[] args) throws IOException { System.out.println("Enter a number:"); int theNumber = getInt(); int theAnswer = triangle(theNumber); System.out.println("Triangle="+theAnswer); } public static int triangle(int n){ System.out.println("Entering: n="+n); if(n==1){ System.out.println("Returning 1"); return 1; } else{ int tem = n+ triangle(n-1); System.out.println("Returning "+tem); return tem; } } public static String getString() throws IOException{ InputStreamReader isr = new InputStreamReader(System.in); BufferedReader br = new BufferedReader(isr); String s = br.readLine(); return s; } public static int getInt() throws IOException{ String s = getString(); return Integer.parseInt(s); } }

12345678910111213141516171819202122232425262728293031323334353637

输入n=5
结果：

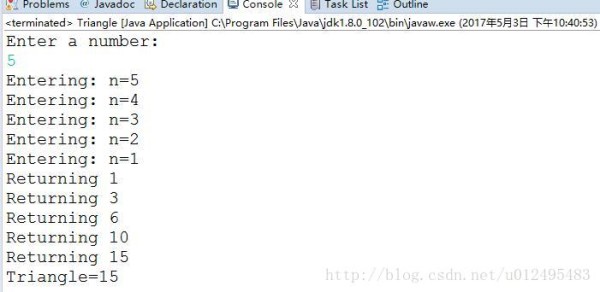
　　在递归中，调用一个方法会存在额外的开销。控制必须保证从调用的位置转移到这个方法的开始处，此外，传给这个方法的参数以及这个方法返回的地址都要被压入到一个内部栈里，当大量数据需要存储，这就会引起栈溢出问题。
2.阶乘
　　与三角数字类似，区别在于：第一点，将三角函数表达式中“+”变成了“*”；第二点，基条件中,当n等于0时，返回结果1。　　

int factorial(int n){ if(n==0) return 1; else return (n*factorial(n-1)); }123456

3.分治算法
1>二分查找
如果用数组采用循环的方式实现二分查找，代码如下。

public int find(int searchKey){ int lowerBound =0; int upperBound = nElems-1; int curIn; while(true){ curIn = (lowerBound+upperBound)/2; if(array[curIn]==searchKey) return curIn; else if(lowerBound>upperBound) return nElems; else{ if(array[curIn]<searchKey) lowerBound = curIn+1; else upperBound = curIn-1; } } }

123456789101112131415161718

现在我们不妨采用递归取代原来的循环，不改变lowerBound或者upperBound，用lowerBound或者upperBound的新值作为参数反复调用find()方法。

private int recFind(int searchKey, int lowerBound, int upperBound){ int curIn; curIn = (lowerBound+upperBound)/2; if(array[curIn]==searchKey){ return curIn; } else if(lowerBound>upperBound) return Elems; else{ if(array[curIn]<searchKey){ return recFind(searchKey,curIn+1,upperBound) } else return recFind(search,lowerBound,curIn-1) } }

12345678910111213141516

现在find()方法中只需要调用recfind()即可

public int Find(int searchKey){ return recFind(searchKey,0,nElems-1); }123

5.汉诺塔(Hanoi)问题
问题描述：
汉诺塔问题是由很多放置在三个塔座上的盘子组成的一个古老的难题。如下图所示，所有盘子直径不同，并且盘子中央都有一个洞以使他们刚好放到塔座上。现在的目标是将所有盘子从初始塔座移动到另一个塔座上，每次只能移动一个盘子，并且任何一个盘子都不可以放在比自己小的盘子上。

汉诺塔

递归的算法：用子树的概念可以递归地表示出汉诺塔难题的解决办法。假设想要把所有的盘子从源塔座S移动到目标塔座D。有一个可以使用的中介塔座I。假定塔座S上有n个盘子。算法如下：
1.从塔座S移动包含上面n-1个盘子到子树塔座I上(可以永远将S中的盘子看成两部分)。
2.从塔座S移动剩余最大的盘子到塔座D上。
3.从塔座I上移动子树到塔座D上。
代码如下

public class TowerTest { static int nDisk=2; public static void main(String[] args) { doTowers(nDisk,'A','B','C'); } public static void doTowers(int topN, char from, char inter, char to){ if(topN==1) System.out.println("Disk 1 from "+from+" to "+to); else{ doTowers(topN-1,from,to,inter); System.out.println("Disk "+topN+" from "+from+" to "+to); doTowers(topN-1,inter,from,to); } } }

1234567891011121314151617

结果：

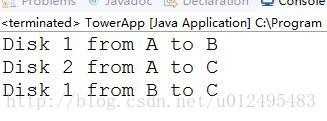
6.归并排序
归并算法的前提是两个数组已经有序，将它们归并在第三个数组中。由此可见归并排序需要一个大小等于被排序数据项数目的数组。通过递归进行排序的思想是把一个数组分成两半，排序每一半，然后用merge()方法把数组的两半归并成一个有序的数组。类似的一半可以继续分成一半，直到只剩一个数字，才返回，并把这两个数据项归并到一个有两个数据项的有序数组中。归并代码如下：

public class MergeSortApp { public static void main(String[] args) { int maxSize = 100; DArray arr = new DArray(maxSize); arr.insert(3); arr.insert(2); arr.insert(99); arr.insert(11); arr.insert(32); arr.insert(51); arr.insert(14); arr.insert(35); arr.insert(51); arr.insert(21); arr.insert(13); arr.insert(25); arr.display(); arr.mergeSort(); arr.display(); } } class DArray{ private int[] theArray; private int nElems; public DArray(int max){ theArray = new int[max]; nElems=0; } public void insert(int value){ theArray[nElems++]=value; } public void display(){ for(int i=0;i<nElems;i++) System.out.print(theArray[i]+" "); System.out.println(""); } public void mergeSort(){ int[] workSpace = new int[nElems]; recMergeSort(workSpace,0,nElems-1); } public void recMergeSort(int[] workSpace, int lowerBound, int upperBound){ if(lowerBound == upperBound) return; else{ int mid = (lowerBound+upperBound)/2; recMergeSort(workSpace,lowerBound,mid); recMergeSort(workSpace,mid+1,upperBound); merge(workSpace,lowerBound,mid+1,upperBound); } } public void merge(int[] workSpace,int lowPtr, int highPtr, int upperBound){ int j=0; int lowerBound = lowPtr; int mid = highPtr-1; int n = upperBound-lowerBound+1; while(lowPtr<=mid&&highPtr<=upperBound){ if(theArray[lowPtr]<theArray[highPtr]) workSpace[j++]=theArray[lowPtr++]; else workSpace[j++]=theArray[highPtr++]; } while(lowPtr<=mid) workSpace[j++]=theArray[lowPtr++]; while(highPtr<=upperBound) workSpace[j++]=theArray[highPtr++]; for(j=0;j<n;j++) theArray[lowerBound+j]=workSpace[j]; } }

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687

运行结果：

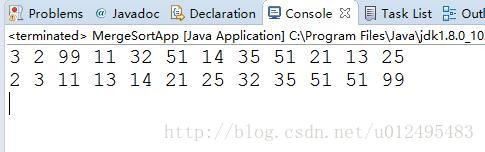
至此递归的典型应用暂时告一段落，以后笔者如果遇到更多递归的案例将会继续更新。

网址：递归及典型应用 https://www.yuejiaxmz.com/news/view/1437557

相关内容

大臣的旅行费用与递归
Python中递归阶乘
广州市节能减排技术应用典型案例（2022年）
递归(一)几个简单的递归例子
从“数学归纳法”到理解“递归算法”！
广东广州公布节能减排技术应用典型案例（2024年）
递归优化技巧
经典神经网络模型的介绍及应用
利用斐波那契数列测试递归及非递归算法的时间复杂度（工具：VS2015、C++，赠送精确计算耗时的类代码）
python编程——006实战递归

随便看看