【转载】C语言中float向double的提升问题，float向double对阶问题

情绪管理：学习正向思考，用积极语言面对问题 #生活技巧# #心理调适技巧# #心理健康资讯#

原文地址：从一个笔试题看C语言中float向double的提升问题 作者：lvyilong316

首先看一段来自一个笔试题的程序段：

float f=1.1;

double d=1.1;

cout<<(f==d)<  

cpp

运行

这段代码输出0，那么为什么同为1.1的doble和float不相等呢？

我们知道float和double比较的时候后发生类型提升，也就是float会提升为double。我们先来看一下这样的情况：

float f=1.1;

double d=1.1;

double d1=f;

cpp

运行

可以发现当由float提升到double后值发生了变化，这究竟是怎么回事呢？我们可以看一下这几个数字的十六进制表示，修改程序如下：

void show_bytes(unsigned char* start,int len)

{

for(int i=0;i<len;i++)

printf("%x ",start[i]);

printf("\n");

}

int _tmain(int argc, _TCHAR* argv[])

{

float f=1.1;

show_bytes((unsigned char*)&f,sizeof(f));

double d=1.1;

show_bytes((unsigned char*)&d,sizeof(d));

double d1=f;

show_bytes((unsigned char*)&d1,sizeof(d1));

return 0;

}

cpp

运行

输出结果：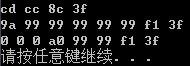

输出结果分别为f、d、d1的十六进制表示，由于所用机器是32位小端方式存放字节，所以这三个数的十六进制表示应为：

f=0x3f 8c cc cd;

d=0x3f f1 99 99 99 99 99 9a;

d1=0x3f f1 99 99 a0 0 0 0;

下面按照IEEE 754的标准对三个数的二进制进行分析：

l f=0011 1111 1000 1100 1100 1100 1100 1101   

对于单精度浮点数：

(1) 符号s 1位：0代表整数；

(2) 阶码E 8位：01111111代表0；(注意阶码的表示方式：对于e的为模式既不全为0也不全为1的情况，E=e-Bias，Bias为2k-1-1，对于单精度是127，双精度是1023)

(3) 尾数M  23位：000 1100 1100 1100 1100 1101代表1+2-4+2-5+2-8+….(注意尾数的表示方式M=1+f，f=0.fn-1…f1f0)

所以这个数的实际值为。

l d=0011 1111 1111 0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010

对于双精度浮点数：

(1) 符号s 1位：0代表整数；

(2) 阶码E 11位：01111111111代表0；(注意阶码的表示方式：对于e的为模式既不全为0也不全为1的情况，E=e-Bias，Bias为2k-1-1，对于单精度是127，双精度是1023)

(3) 尾数M  52位：0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010代表1+2-4+2-5+2-8+….(注意尾数的表示方式M=1+f，f=0.fn-1…f1f0)，可以看出双进度的尾数要比单精度尾数更加精确。

所以这个数的实际值也为。

但是要注意虽然d和f都约为1.1，但实际值是不相等的，d要比f更加接近于1.1，因为d的尾数有更高的精度。

l d1=0011 1111 1111 0001 1001 1001 1001 1001 1010 0000 0000 0000….

对于双精度浮点数：

(1) 符号s 1位：0代表整数；

(2) 阶码E 11位：01111111111代表0；(注意阶码的表示方式：对于e的为模式既不全为0也不全为1的情况，E=e-Bias，Bias为2k-1-1，对于单精度是127，双精度是1023)

(3) 尾数M  52位：0001 1001 1001 1001 1001 1010 0000 0000 0000….代表1+2-4+2-5+2-8+….(注意尾数的表示方式M=1+f，f=0.fn-1…f1f0)。

重点出现了：可以看出d1的阶码的值和f、d都是一样的，但是尾数M和d不同，对比f的尾数000 1100 1100 1100 1100 1101发现和d1的值是相同的，只是后面补了些0。也就是说float提升为double数的精度并没有提高(值没变),既然精度没有提高那和d肯定是不相等的，因为d比f和d1有更高的精度，更接近于1.

为了验证float提升为double后值没有改变，有如下语句：

cout<<(d1==f)<  //输出1

同时我们可以得到如下结论：

(1) float提升为double，是对阶码E和尾数M的扩展；

(2) 阶码E和尾数M的扩展方式都按照”保持值不变”的原则扩展。

(3) float提升为double后值保持不变，精度不增加。

有了以上结论，我们将上述程序中的1.1改为1.5,猜想下f、d、d1之间相等吗？代码如下：

点击(此处)折叠或打开

int _tmain(int argc, _TCHAR* argv[])

{

float f=1.5;

show_bytes((unsigned char*)&f,sizeof(f));

double d=1.5;

show_bytes((unsigned char*)&d,sizeof(d));

double d1=1.5;

show_bytes((unsigned char*)&d1,sizeof(d1));

  cout<<(d==d1)<<endl;

  cout<<(f==d)<<endl;

return 0;

}

cpp

运行

运行结果：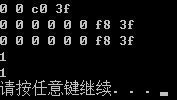

可以看到f、d、d1都是相等的，因为1.5用浮点数是可以精确表示的，所以float的1.5和double的1.5都是准确的1.5，所以float提升为double依然是准确的1.5，当然三个数相等。而float的1.1提升为double后和double的1.1不等的原因归根结底是因为1.1不能用浮点数精确表示，float的1.1和double的1.1就不想等，float提升后值不变依然不等。

网址：【转载】C语言中float向double的提升问题，float向double对阶问题 https://www.yuejiaxmz.com/news/view/1444049

相关内容

C语言学习错题集（一）
（dataframe string 转 float）（object 转 float）
【Java】基础类型之float（八）
C语言基础
日常生活中，我们接触到的算法无处不在，驱动着智能手机、社交媒体、导航、购物等各种应用。这些算法通常在后台运行，优化用户体验、提高效率或提供个性化服务
如何用c语言解决日常生活问题
n=sizeof(a)/sizeof(int)的含义（C语言）
用C#编写简易贷款计算器
2018.11.14信息学奥赛辅导 向上取整
java数据类型04

随便看看